早教吧作业答案频道 -->数学-->
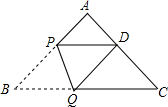
如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D(不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为.
题目详情
如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D (不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为___.

▼优质解答
答案和解析
①PD=DQ时,BP=BQ,
由翻折变换得,BP=PD,BQ=DQ,
所以,BP=BQ=PD=DQ,
所以,四边形BQDP是菱形,
所以,PD∥BC,BP∥DQ,
∵∠A=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴△APD和△CDQ都是等腰直角三角形,
在Rt△APD中,PD=
AD,
在Rt△CDQ中,CD=DQ,
∵PD=DQ,
∴CD=
AD,
∵AC=AD+CD,
∴AD+
AD=2,
解得AD=2
-2;
②DQ=PQ时,BQ=PQ,
所以,∠BPQ=∠B=45°,
所以,△BPQ是等腰直角三角形,
所以,点B与点C重合,
所以,AD=AC=2;
③PD=PQ时,PQ=BP,
所以,∠BQP=∠B=45°,
所以,△BPQ是等腰直角三角形,
所以,点B与点A重合,
此时,点B与点A重合,不符合题意,舍去;
综上所述,AD的长度为2或2
-2.
故答案为:2或2
-2.
由翻折变换得,BP=PD,BQ=DQ,
所以,BP=BQ=PD=DQ,
所以,四边形BQDP是菱形,
所以,PD∥BC,BP∥DQ,
∵∠A=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴△APD和△CDQ都是等腰直角三角形,
在Rt△APD中,PD=
| 2 |
在Rt△CDQ中,CD=DQ,
∵PD=DQ,
∴CD=
| 2 |
∵AC=AD+CD,
∴AD+
| 2 |
解得AD=2
| 2 |
②DQ=PQ时,BQ=PQ,
所以,∠BPQ=∠B=45°,
所以,△BPQ是等腰直角三角形,
所以,点B与点C重合,
所以,AD=AC=2;
③PD=PQ时,PQ=BP,
所以,∠BQP=∠B=45°,
所以,△BPQ是等腰直角三角形,
所以,点B与点A重合,
此时,点B与点A重合,不符合题意,舍去;
综上所述,AD的长度为2或2
| 2 |
故答案为:2或2
| 2 |
看了 如图,在三角形ABC中,∠A...的网友还看了以下:
如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、 2020-06-13 …
请用两种方法解答下列问题:海伦-秦九韶公式:如果一个三角形三边长分别为a,b,c,设p=a+b+c 2020-06-14 …
为什么s能级为球形?p能级为纺锤形? 2020-06-21 …
用向量方法可以证明:若P为正三角形内切圆上任意一点,则点P到三角形三个顶点距离的平方和为定值.请你 2020-07-31 …
如图,点M是矩形ABCD的边AD的中点.点P是BC边上一动点,PE⊥MC,PF⊥BM.垂足为E、F 2020-08-03 …
四边形ABCD是矩形,点P为矩形所在平面内任意一点,连接PA、PB、PC、PD.(1)如图1,当点P 2020-10-30 …
用配方法将关于x的方程x2+5x+n=0可以变形为(x+p)2=9,那么用配方法也可以将关于x的方程 2020-10-31 …
如图,矩形ABCD中,AB=12cm,BC=8cm,E为CD的中点.点P从A点出发,沿A-B-C的方 2020-11-01 …
在美化校园的植树活动中,某同学共种了6棵树,各棵树的成活与否是相互独立的,每棵树成活的概率均为p.已 2020-11-04 …
己知矩形ABCD,P为矩形所在平面内的任意一点,求证:PA2+PC2=PB2+PD2.(提示:应分P 2020-12-25 …