早教吧作业答案频道 -->数学-->
己知矩形ABCD,P为矩形所在平面内的任意一点,求证:PA2+PC2=PB2+PD2.(提示:应分P在矩形内、P在矩形上、P在矩形外,三种情形加以讨论.)
题目详情
己知矩形ABCD,P为矩形所在平面内的任意一点,求证:PA2+PC2=PB2+PD2.(提示:应分P在矩形内、P在矩形上、P在矩形外,三种情形加以讨论.)
▼优质解答
答案和解析
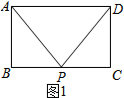 证明:①如图1,P在矩形的边上,
证明:①如图1,P在矩形的边上,
在Rt△ABP中,由勾股定理,得PA2-PB2=AB2,
同理可得PD2-PC2=CD2,
由矩形的性质可得AB=CD,
∴PA2-PB2=PD2-PC2,
∴PA2+PC2=PB2+PD2.
②P在矩形内,如图2,过点P作AD的垂线,交AD于点E,交BC于点F,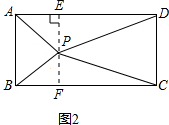
则四边形ABFE和CDEF为矩形,
∴AE=BF,DE=CF,
由勾股定理得:
则AP2=AE2+PE2,PC2=PF2+CF2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AE2+PE2+PF2+CF2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2.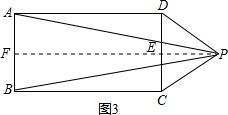
③P在矩形外,如图3,过P作PF⊥AB于F,交CD于E,
则PE⊥CD,
∴四边形AFED与四边形BCEF是矩形,
∴BF=CE,AF=DE,
由勾股定理得:
则AP2=AF2+PF2,PC2=PE2+CE2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AF2+PF2+PE2+CE2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2.
 证明:①如图1,P在矩形的边上,
证明:①如图1,P在矩形的边上,在Rt△ABP中,由勾股定理,得PA2-PB2=AB2,
同理可得PD2-PC2=CD2,
由矩形的性质可得AB=CD,
∴PA2-PB2=PD2-PC2,
∴PA2+PC2=PB2+PD2.
②P在矩形内,如图2,过点P作AD的垂线,交AD于点E,交BC于点F,

则四边形ABFE和CDEF为矩形,
∴AE=BF,DE=CF,
由勾股定理得:
则AP2=AE2+PE2,PC2=PF2+CF2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AE2+PE2+PF2+CF2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2.

③P在矩形外,如图3,过P作PF⊥AB于F,交CD于E,
则PE⊥CD,
∴四边形AFED与四边形BCEF是矩形,
∴BF=CE,AF=DE,
由勾股定理得:
则AP2=AF2+PF2,PC2=PE2+CE2,
BP2=BF2+PF2,PD2=DE2+PE2,
∴PA2+PC2=AF2+PF2+PE2+CE2,
PB2+PD2=BF2+PF2+DE2+PE2,
∴PA2+PC2=PB2+PD2.
看了己知矩形ABCD,P为矩形所在...的网友还看了以下:
暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的 2020-04-27 …
有矩体这个说法吗矩形的矩,矩形为什么到初中就不能叫长方形了呢?另外长方体可以说成矩体吗 2020-06-20 …
(1)七巧板的2块部件能组成一个三角形吗?3块呢?5块呢?6块呢?7块呢?(2)用2块部件能组成正 2020-07-14 …
在0.10mo1·L–1的Mn2+溶液中含有少量的Pb2+,现欲使Pb2+形成PbS沉淀除去,而M 2020-07-19 …
在三角形ABC中有一内接矩形,矩形的一边EF在BC上两顶点H、G分别在AB、AC上,若HE:HG= 2020-07-30 …
关于矩阵的初等变换化成行阶梯形矩阵的问题,怎样判断是否化成了行阶梯形矩阵?又时候明明化成了书上定义 2020-08-02 …
形容一个人一时取得成功很受瞩目,但很快就消失在人们的视野中的,用什么形容词要一个词语,比如说要成功就 2020-11-22 …
大雾形成的条件中与深秋初冬季节相关的是()A.昼夜温差较小,水汽易凝结形成B.昼夜温差较小,水汽不易 2020-12-07 …
关于校运会队形变换(在线等,一定要快)校运会开始了,我们班是二班,有50人,队形排列要新颖,要创新, 2020-12-25 …
(1)正方形ABCD对角线为6根号2,点E是CD上一点,CE=2根号3,求角BED度数(2)正方形A 2020-12-25 …