早教吧作业答案频道 -->数学-->
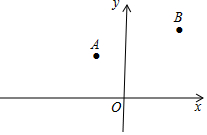
如图,在平面直角坐标系中,点A(-2,3),B(4,5),点P是x轴上一动点.求:①PA+PB的最小值及此时点P的坐标;②|PA-PB|的最大值及此时点P的坐标.
题目详情
如图,在平面直角坐标系中,点A(-2,3),B(4,5),点P是x轴上一动点.求:
①PA+PB的最小值及此时点P的坐标;
②|PA-PB|的最大值及此时点P的坐标.
①PA+PB的最小值及此时点P的坐标;
②|PA-PB|的最大值及此时点P的坐标.

▼优质解答
答案和解析
(1)如图1所示:作点A关于x轴的对称点A′,连结A′B交x轴与点P.
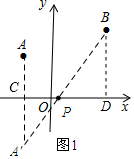
∵点A′关于点A对称,
∴点A′的坐标为(-2,-3).
∴AP+BP=A′P+PB=A′B=10.
∴PA+PB的最小值为10.
过点B作BD⊥x轴垂足为D.
∵△CPA′∽△DPB,
∴CP:DP=CA′:BD=3:5.
又∵CD=6,
∴CP=6×
=
.
∴OP=
.
∴点P的坐标为(
,0).
(2)如图2所示,作直线AB与x轴交与点P,作AC⊥x轴,BD⊥x轴.
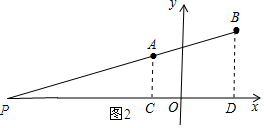
当点P在直线AB上时,|PA-PB|的最大值=AB=
=2
.
∵AC∥BD,
∴△PAC∽△PBD.
∴
=
即
=
.
解得PC=9.
∴PO=9+2=11.
∴点P的坐标为(-11,0).

∵点A′关于点A对称,
∴点A′的坐标为(-2,-3).
∴AP+BP=A′P+PB=A′B=10.
∴PA+PB的最小值为10.
过点B作BD⊥x轴垂足为D.
∵△CPA′∽△DPB,
∴CP:DP=CA′:BD=3:5.
又∵CD=6,
∴CP=6×
| 3 |
| 8 |
| 9 |
| 4 |
∴OP=
| 1 |
| 4 |
∴点P的坐标为(
| 1 |
| 4 |
(2)如图2所示,作直线AB与x轴交与点P,作AC⊥x轴,BD⊥x轴.

当点P在直线AB上时,|PA-PB|的最大值=AB=
| 62+22 |
| 10 |
∵AC∥BD,
∴△PAC∽△PBD.
∴
| PC |
| PD |
| PA |
| PB |
| PC |
| PC+6 |
| 3 |
| 5 |
解得PC=9.
∴PO=9+2=11.
∴点P的坐标为(-11,0).
看了 如图,在平面直角坐标系中,点...的网友还看了以下:
已知一次函数的图像经过点(2,1),b(-1,-3).求求此一次函数与x轴和y轴的交点坐标及一次函 2020-04-08 …
一直一次函数的图像进过点(2,1)和(-1,-3)(1)求此一次函数解析式(2)求此一次函数与X轴 2020-04-08 …
一道奇怪的数学题考察所有可能的这样的抛物线,y=x²+ax-b²:它们同坐标轴各有3个不同的交点, 2020-05-14 …
如图,抛物线y=ax2+bx+c交坐标轴于点A(-1,0)、B(3,0)、C(0,-3)。(1)求 2020-05-17 …
一道怪题,我从没碰到过考察所有可能的这样的抛物线,y=x²+ax-b²:它们同坐标轴各有3个不同的 2020-05-20 …
已知一次函数的图像经过点(2,1)和(-1,-3)1.求此一次函数的解析式2.求此一次函数的图像与 2020-07-01 …
已知下列命题:①同位角相等;②若a>b>0,则1a<1b;③对角线相等且互相垂直的四边形是正方形; 2020-07-23 …
已知一次函数的图象经过点(2,1),(-1,-3)1·求此一次函数解析式2·求此一次函数于X,Y轴 2020-07-25 …
已知一次函数的图象经过点(2,1),(-1,-3)1·求此一次函数解析式2·求此一次函数于X,Y轴 2020-07-25 …
己知一次凼数的图像经过点(2,1)和(-1,-3).(1)求此一次函数的解析式;(2)求此一次函数与 2020-12-25 …