早教吧作业答案频道 -->数学-->
如图,菱形ABCD中,∠ABC=60°,E是射线CB上一点,F是CD上一点,且∠EAF=120°.(1)如图1,求证:AEAF=ABCF;(2)如图2,若△CEF的面积为23,求AB的长;(3)如图3,求证:BF∥DE.
题目详情
如图,菱形ABCD中,∠ABC=60°,E是射线CB上一点,F是CD上一点,且∠EAF=120°.
(1)如图1,求证:
=
;
(2)如图2,若△CEF的面积为2
,求AB的长;
(3)如图3,求证:BF∥DE.
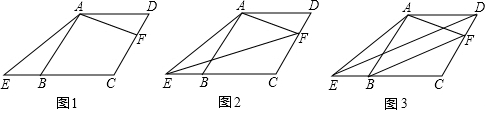
(1)如图1,求证:
| AE |
| AF |
| AB |
| CF |
(2)如图2,若△CEF的面积为2
| 3 |
(3)如图3,求证:BF∥DE.

▼优质解答
答案和解析
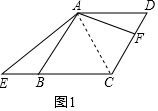
 (1)如图1,连接AC,
(1)如图1,连接AC,
∵在菱形ABCD中,∠ABC=60°,
∴∠D=60°,△ACB是等边三角形,
∴∠BAC=60°,
∵∠EAF=120°,
∴∠EAB=∠DAF,
∵∠EAC=60°+∠EAB,∠AFC=60°+∠DAF,
∴∠EAC=∠AFC,
∵∠ACE=∠ACF=60°,
∴△ACE∽△CAF,
∴
=
,
∵AB=AC,
∴
=
;
(2)由(1)知
=
,
∴AC2=CE•CF,
如图2,过F作FM⊥CE于M交EC的延长线于M,
可得FM=
CF,
∵△CEF的面积为2
,
即
CE•FM=
CE•
CF=2
,
∴CE•CF=8,
即AC2=AB2=8,
∴AB=2
;
(3)由(1)有
=
,
易知AC=AB=BC=CD,
∴
=
,
即
=
,
∵∠BCF=∠ECD,
∴△CBF∽△CED,
∴∠CBF=∠CED,
∴BF∥ED.

 (1)如图1,连接AC,
(1)如图1,连接AC,∵在菱形ABCD中,∠ABC=60°,
∴∠D=60°,△ACB是等边三角形,
∴∠BAC=60°,
∵∠EAF=120°,
∴∠EAB=∠DAF,
∵∠EAC=60°+∠EAB,∠AFC=60°+∠DAF,
∴∠EAC=∠AFC,
∵∠ACE=∠ACF=60°,
∴△ACE∽△CAF,
∴
| AE |
| AF |
| AC |
| CF |
∵AB=AC,
∴
| AE |
| AF |
| AB |
| CF |
(2)由(1)知
| AC |
| CF |
| CE |
| AC |
∴AC2=CE•CF,
如图2,过F作FM⊥CE于M交EC的延长线于M,
可得FM=
| ||
| 2 |
∵△CEF的面积为2
| 3 |
即
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴CE•CF=8,
即AC2=AB2=8,
∴AB=2
| 2 |
(3)由(1)有
| AC |
| CF |
| CE |
| AC |
易知AC=AB=BC=CD,
∴
| CD |
| CF |
| CE |
| BC |
即
| CF |
| CD |
| CB |
| CE |
∵∠BCF=∠ECD,
∴△CBF∽△CED,
∴∠CBF=∠CED,
∴BF∥ED.
看了 如图,菱形ABCD中,∠AB...的网友还看了以下:
在直角坐标系中有点A(a,b),B(a,c),C(-a,-b),D(-a,-c)(a≠0,b≠c) 2020-04-27 …
已知向量a,b,c满足|a|=1,|a-b|=|b|,(a-c)(b-c)=0.若对每一确定的b, 2020-05-16 …
在直角坐标系中有点A(a.b)B(a.c)C(-a.-b)D(-a.-c)(a≠0b≠c)若要使四 2020-05-19 …
正弦定理问题在三角形ABC中,若(a+b)(sinB-sinA)=a(sinB),且cos2C+c 2020-05-20 …
两道集合论的题1设ABC是全集U的任意子集.a)若A∩B=A∩C,A∩B=~A∩C,证明:B=Cb 2020-06-07 …
用向量证明余弦定理a、b、c都表示向量,|a|、|b|、|c|表示向量的模因为a=b-c所以a^2 2020-07-07 …
1.在三角形abc中,证明a/b-b/a=c(CosB/b-CosA/a)2.在三角形abc中,已 2020-07-21 …
实数的乘法运算与向量的数量积运算类比,不成立的运算律是()。A.a×b=b×a类比a→⋅b→=b→ 2020-07-31 …
在平面直角坐标系中,o为坐标原点,已知点A(0,a),B(b,b),C(c,a),其中a,b满足关 2020-08-02 …
1从a+b=b+c,能否得到a=c,为什么?2从a-b=c-b,能否得到a=c,为什3从ab=bc, 2020-10-30 …