早教吧作业答案频道 -->数学-->
如图,已知二次函数y1=-x2+134x+c的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为y2=kx+b.(1)求二次函数y1的解析式及点B的坐标;(2)由图象写出满足y1<y2的自变量x的
题目详情
如图,已知二次函数y1=-x2+
x+c的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为y2=kx+b.
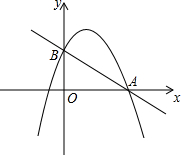
(1)求二次函数y1的解析式及点B的坐标;
(2)由图象写出满足y1<y2的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出P的坐标;若不存在,说明理由.
| 13 |
| 4 |

(1)求二次函数y1的解析式及点B的坐标;
(2)由图象写出满足y1<y2的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出P的坐标;若不存在,说明理由.
▼优质解答
答案和解析
(1)将A点坐标代入y1,得
-16+13+c=0.
解得c=3,
二次函数y1的解析式为y=-x2+
x+3,
B点坐标为(0,3);
(2)由图象得直线在抛物线上方的部分,是x<0或x>4,
∴x<0或x>4时,y1<y2;
(3)直线AB的解析式为y=-
x+3,
AB的中点为(2,
)
AB的垂直平分线为y=
x-
当x=0时,y=-
,P1(0,-
),
当y=0时,x=
,P2(
,0),
综上所述:P1(0,-
),P2(
,0),使得△ABP是以AB为底边的等腰三角形.
-16+13+c=0.
解得c=3,
二次函数y1的解析式为y=-x2+
| 13 |
| 4 |
B点坐标为(0,3);
(2)由图象得直线在抛物线上方的部分,是x<0或x>4,
∴x<0或x>4时,y1<y2;
(3)直线AB的解析式为y=-
| 3 |
| 4 |
AB的中点为(2,
| 3 |
| 2 |
AB的垂直平分线为y=
| 4 |
| 3 |
| 7 |
| 6 |
当x=0时,y=-
| 7 |
| 6 |
| 7 |
| 6 |
当y=0时,x=
| 7 |
| 8 |
| 7 |
| 8 |
综上所述:P1(0,-
| 7 |
| 6 |
| 7 |
| 8 |
看了 如图,已知二次函数y1=-x...的网友还看了以下:
求线性代数一道题,已知3维列向量α,β满足α^Tβ=3,设三阶矩阵A=βα^T,则Aβ为满足A的特 2020-04-13 …
在平面直角坐标系中,O为坐标原点,A,B,C三点满足向量OC = 2/3 向量OA + 1/3在平 2020-05-16 …
甲乙两车分别从AB两地出发,相向而行,在距A地40km处第一次相遇,到达目的地后立即返回,在距B点 2020-06-14 …
这道题是应用题!商店购物a店五点五折,b点满100元送100元购物券.若买上衣280元裤子20元一 2020-06-30 …
如图,在数轴上A点表示数a,B点表示数b,C点表示数c.且a、c满足|a+3|+(c-7)2=0. 2020-07-30 …
沿x轴正方向运动的A质点和B质点,其位置-时间图象(如图所示)分别为图中直线a和曲线b,已知B质点 2020-07-31 …
已知A是最大的负整数,且a,b,c满足|a+b|+(c-4)²=0(1)点a,b,c分别表示(1)中 2020-11-18 …
如图所示,在同一竖直线上有A、B两点,相距为h,B点离地高度为H,现在要在地面上寻找一点P,使得从A 2020-12-06 …
1.已知点P为三角形ABO所在平面内的一点,满足向量OP=向量OA/|向量OA|+向量OB/|向量O 2020-12-07 …
答好给40分,说话算数的!设三角形ABC的三内角A,B,C满足2B=A+C,a,b,c分别是内角A, 2020-12-23 …