早教吧作业答案频道 -->数学-->
设抛物线x=2pt2y=2pt(t为参数,p>0)的焦点为F,准线为l,过抛物线上一点A作l的垂线,垂
题目详情
设抛物线
(t为参数,p>0)的焦点为F,准线为l,过抛物线上一点A作l的垂线,垂足为B,设C(
p,0),AF与BC相交于点E.若|CF|=2|AF|,且△ACE的面积为3
,则p的值为___.
| |
|
| 7 |
| 2 |
| | 2 |
▼优质解答
答案和解析
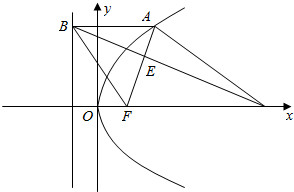 抛物线
抛物线
(t为参数,p>0)的普通方程为:y2=2px焦点为F(
,0),如图:过抛物线上一点A作l的垂线,垂足为B,设C(
p,0),AF与BC相交于点E.|CF|=2|AF|,
|CF|=3p,|AB|=|AF|=
p,A(p,
p),
△ACE的面积为3
,
=
=
,
可得
S△AFC=S△ACE.
即:
×
×3p×
p=3
,
解得p=
.
故答案为:
.
 抛物线
抛物线
|
| p |
| 2 |
| 7 |
| 2 |
|CF|=3p,|AB|=|AF|=
| 3 |
| 2 |
| 2 |
△ACE的面积为3
| 2 |
| AE |
| EF |
| AB |
| CF |
| 1 |
| 2 |
可得
| 1 |
| 3 |
即:
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
解得p=
| 6 |
故答案为:
| 6 |
看了 设抛物线x=2pt2y=2p...的网友还看了以下:
已知M是抛物线C:x^2=4y上的动点,过M作y轴的垂线MN,垂足为N,记线段MN的中点为E.(1 2020-04-13 …
已知M是抛物线C:x^2=4y上的动点,过M作y轴的垂线MN,垂足为N,记线段MN的中点为E.(1 2020-04-13 …
若过两抛物线y=x^2-2x+2和y=-x^2+ax+b的一个交点为P的两条切线互相垂直.求证:抛 2020-05-20 …
高手进,急需!抛物线!设λ>0,点A得坐标为(1,1),点B在抛物线y=x²上运动,点Q满足向量B 2020-05-23 …
如图,已知直线y=x+2与两坐标轴分别交于A、B两点,抛物线y=x2+bx+c经过点A、B,P为直 2020-06-14 …
一道二次函数小题已知抛物线y=-x^2+2x.过抛物线上一点P(x,y)向直线y=5/4做垂线,垂 2020-07-14 …
已知抛物线y=-x^2+2x.过抛物线上一点P(x,y)向直线y=5/4做垂线,垂足为M.请问:对 2020-07-14 …
已知抛物线y=-x^2+2mx-m^2+2的顶点A在第一象限,过点A作AB垂直y轴,垂足为B,C是A 2020-11-28 …
如图,已知直线y=x+2与两坐标轴分别交与A、B两点,抛物线y=x2+bx+c经过点A、B,P为直线 2021-01-10 …
y=x(X的平方)-4x+3与坐标轴交与A,B,C三点,点P为抛物线上一点,PE垂直于BC与E点,且 2021-01-11 …