早教吧作业答案频道 -->数学-->
如图,直线y=k1x+7(k1<0)与x轴交于点A,与y轴交于点B,与反比例函数y=k2x(k2>0)的图象在第一象限交于C、D两点,点O为坐标原点,△AOB的面积为492,点C横坐标为1.(1)求反比例函数的
题目详情
如图,直线y=k1x+7(k1<0)与x轴交于点A,与y轴交于点B,与反比例函数y=
(k2>0)的图象在第一象限交于C、D两点,点O为坐标原点,△AOB的面积为
,点C横坐标为1.
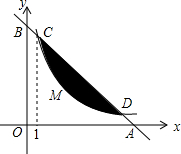
(1)求反比例函数的解析式;
(2)如果一个点的横、纵坐标都是整数,那么我们就称这个点为“整点”,请求出图中阴影部分(不含边界)所包含的所有整点的坐标.
| k2 |
| x |
| 49 |
| 2 |

(1)求反比例函数的解析式;
(2)如果一个点的横、纵坐标都是整数,那么我们就称这个点为“整点”,请求出图中阴影部分(不含边界)所包含的所有整点的坐标.
▼优质解答
答案和解析
(1)∵当x=0时,y=7,当y=0时,x=-
,
∴A(-
,0)、B(0、7).
∴S△AOB=
|OA|•|OB|=
×(-
)×7=
,解得k1=-1.
∴直线的解析式为y=-x+7.
∵当x=1时,y=-1+7=6,
∴C(1,6).
∴k2=1×6=6.
∴反比例函数的解析式为y=
.
(2)∵点C与点D关于y=x对称,
∴D(6,1).
当x=2时,反比例函数图象上的点为(2,3),直线上的点为(2,5),此时可得整点为(2,4);
当x=3时,反比例函数图象上的点为(3,2),直线上的点为(3,4),此时可得整点为(3,3);
当x=4时,反比例函数图象上的点为(4,
),直线上的点为(4,3),此时可得整点为(4,2);
当x=5时,反比例函数图象上的点为(5,
),直线上的点为(5,2),此时,不存在整点.
综上所述,符合条件的整点有(2,4)、(3,3)、(4,2).
| 7 |
| k1 |
∴A(-
| 7 |
| k1 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| k1 |
| 49 |
| 2 |
∴直线的解析式为y=-x+7.
∵当x=1时,y=-1+7=6,
∴C(1,6).
∴k2=1×6=6.
∴反比例函数的解析式为y=
| 6 |
| x |
(2)∵点C与点D关于y=x对称,
∴D(6,1).
当x=2时,反比例函数图象上的点为(2,3),直线上的点为(2,5),此时可得整点为(2,4);
当x=3时,反比例函数图象上的点为(3,2),直线上的点为(3,4),此时可得整点为(3,3);
当x=4时,反比例函数图象上的点为(4,
| 3 |
| 2 |
当x=5时,反比例函数图象上的点为(5,
| 6 |
| 5 |
综上所述,符合条件的整点有(2,4)、(3,3)、(4,2).
看了 如图,直线y=k1x+7(k...的网友还看了以下:
已知函数f(x)=sin(x-13π2)(x∈R),下面结论错误的是()A.函数f(x)的最小正周 2020-04-12 …
已知函数f(x)=2^(x^2;-ax-3)是偶函数,试确定a的值及此时的函数解析式;证明函数f( 2020-04-27 …
下列命题中正确的是()A.当α=0时函数y=xα的图象是一条直线B.幂函数的图象都经过(0,0)和 2020-05-13 …
下列命题中的真命题的序号为.①函数y=1x的单调递减区间是(-∞,0)∪(0,+∞).②当n>0时 2020-05-13 …
定义在R上的函数f(x),对任意x,y∈R,有f(x+y)+f(x-y)=2f(x)*f(y),且 2020-05-13 …
设函数f(x)在x=0的某邻域具有二阶连续导数,且f(0)f′(0)f″(0)≠0.证明:存在惟一 2020-07-13 …
下列命题中正确的是()A.当α=0时函数y=xα的图象是一条直线B.幂函数的图象都经过(0,0)和 2020-08-01 …
如图,空间直角坐标系O-xyz中,已知A(1,0,0),B(0,2,0),现将△AOB按向量p=(0 2020-11-07 …
在指数函数中a^0则a的取值范围是a不等于0还是a大于o?指数函数中负数的0次方无意义,所以是否要a 2020-12-09 …
已知二次函数g(x)=mx2-2mx+n+1(m>0)在区间[0,3]上有最大值4,最小值0.(Ⅰ) 2020-12-27 …