如图，动点M在以O为圆心，AB为直径的半圆弧上运动（点M不与点A、B及AB的中点F重合），连接OM．过点M作ME⊥AB于点E，以BE为边在半圆同侧作正方形BCDE，过点M作⊙O的切线交射线DC于点N，连

Question

如图，动点M在以O为圆心，AB为直径的半圆弧上运动（点M不与点A、B 及

AB

的中点F 重合），连接OM．过点M 作ME⊥AB于点E，以BE为边在半圆同侧作正方形BCDE，过点M作⊙O的切线交射线DC于点N，连接BM、BN．

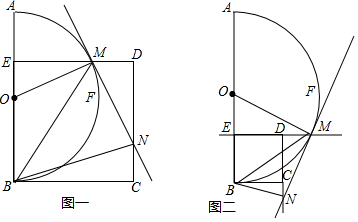
（1）探究：如图一，当动点M在

AF

上运动时；
①判断△OEM∽△MDN是否成立？请说明理由；
②设(ME+NC)/(MN)=k，k是否为定值？若是，求出该定值，若不是，请说明理由；
③设∠MBN=α，α是否为定值？若是，求出该定值，若不是，请说明理由；
（2）拓展：如图二，当动点M 在

FB

上运动时；
分别判断（1）中的三个结论是否保持不变？如有变化，请直接写出正确的结论．（均不必说明理由）

Answer 1

（1）①△OEM∽△MDN成立，理由如下：
∵四边形BCDE是正方形，
∴BE=BC，∠EBC=∠CDE=∠BCD=∠BED=90°，
∴∠EOM+∠EMO=90°，
∵MN是⊙O的切线，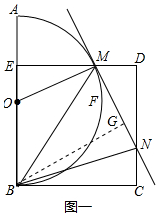
∴MN⊥OM，
∴∠OMN=90°，
∴∠DMN+∠EMO=90°，
∴∠EOM=∠DMN，
∴△OEM∽△MDN；
②k值为定值1；理由如下：
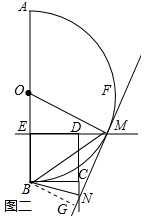
作BG⊥MN于G，如图一所示：
则BG∥OM，∠BGN=∠BGM=90°，
∴∠OMB=∠GBM，
∵OB=OM，
∴∠OBM=∠OMB，
∴∠OBM=∠GBM，
在△BME和△BMG中，

∠OBM=∠GBM

∠BED=∠BGM=90°

BM=BM

，
∴△BME≌△BMG（AAS），
∴EM=GM，BE=BG，
∴BG=BC，
在Rt△BGN和Rt△BCN中，

BN=BN

BG=BC

，
∴Rt△BGN≌Rt△BCN（HL），
∴GN=CN，
∴EM+NC=GM+NC=MN，
∴k=(ME+NC)/(MN)=(MN)/(MN)=1；
③设∠MBN=α，α为定值45°；理由如下：
∵△BME≌△BMG，Rt△BGN≌Rt△BCN，
∴∠EBM=∠GBM，∠GBN=∠CBN，
∴∠MBN=(1)/(2)∠EBC=45°，
即α=45°；
（2）（1）中的三个结论保持不变；理由同（1），作BG⊥MN于G，如图二所示．