早教吧作业答案频道 -->数学-->
如图所示,直线DP和圆O相切于点C,交直线AE的延长线于点P,过点C作AE的垂线,交AE于点F,交圆O于点B,作平行四边形ABCD,连接BE,DO,CO.(1)求证:DA=DC;(2)求∠P及∠AEB的大小.
题目详情
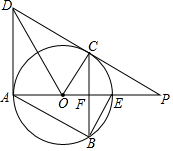
如图所示,直线DP和圆O相切于点C,交直线AE的延长线于点P,过点C作AE的垂线,交AE于点F,交圆O于点B,作平行四边形ABCD,连接BE,DO,CO.
(1)求证:DA=DC;
(2)求∠P及∠AEB的大小.

(1)求证:DA=DC;
(2)求∠P及∠AEB的大小.
▼优质解答
答案和解析
(1)证明:在平行四边形ABCD中,AD∥BC,
∵CB⊥AE,
∴AD⊥AE,
∴∠DAO=90°,
∵DP与⊙O相切于点C,
∴DC⊥OC,
∴∠DCO=90°,
在Rt△DAO和Rt△DCO中,
,
∴Rt△DAO≌△Rt△DCO,
∴DA=DC.
(2)∵CB⊥AE,AE是直径,
∴CF=FB=
BC,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴CF=
AD,
∵CF∥DA,
∴△PCF∽△PDA,
∴
=
=
,
∴PC=
PD,DC=
PD,
∵DA=DC,
∴DA=
PD,
在Rt△DAP中,∠P=30°,
∵DP∥AB,
∴∠FAB=∠P=30°,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠AEB=60°.
∵CB⊥AE,
∴AD⊥AE,
∴∠DAO=90°,
∵DP与⊙O相切于点C,
∴DC⊥OC,
∴∠DCO=90°,
在Rt△DAO和Rt△DCO中,
|
∴Rt△DAO≌△Rt△DCO,
∴DA=DC.
(2)∵CB⊥AE,AE是直径,
∴CF=FB=
| 1 |
| 2 |

∵四边形ABCD是平行四边形,
∴AD=BC,
∴CF=
| 1 |
| 2 |
∵CF∥DA,
∴△PCF∽△PDA,
∴
| PC |
| PD |
| CF |
| DA |
| 1 |
| 2 |
∴PC=
| 1 |
| 2 |
| 1 |
| 2 |
∵DA=DC,
∴DA=
| 1 |
| 2 |
在Rt△DAP中,∠P=30°,
∵DP∥AB,
∴∠FAB=∠P=30°,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠AEB=60°.
看了 如图所示,直线DP和圆O相切...的网友还看了以下:
已知线段AB=6,MN是线段的垂直平分线.点C是MN上一动点,连AC,BC,过A做AD垂直于直线BC 2020-03-31 …
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从 2020-06-02 …
如图,AB为圆O的直径,PB为O的切线,AC//OP,点C在圆O上,OP交圆O于D,DA交BC于G 2020-06-27 …
圆O的半径r为13厘米,圆心O到直线l的距离OD为5厘米,点A,B,C在直线上若DA=13,则点A 2020-07-26 …
在矩形ABCD中,AB=4,AD=6,点P是射线DA上的一个动点,将三角板的直角顶点重合于点P,三 2020-07-30 …
A,B,C三点共线,点C分有向线段AB所成比为-3,则B点分有向线段AC所成比为这是一条数学题,本 2020-08-02 …
关于双焦眼镜子片光学中心位置的描述包括()。A.偏离近视线点B.近视线点C.不在眼镜框内D.1/2顶 2020-08-22 …
如图所示,铁路上A、B两站(视为线上两点)相距25km,C、D为铁路同旁的两个村庄(视为两点),DA 2020-11-20 …
如图,已知等腰三角形ABC的直角边AC=BC=a,等腰直角三角形BED的指教边BE=DE=b,且a小 2020-12-07 …
采用如下方法可以得到黄金分割点:如图,设AB是已知线段,经过点B作BD⊥AB,使BD=12AB,连接 2021-01-06 …