早教吧作业答案频道 -->数学-->
如图,在△BCE中,点A是边BE上一点,以AB为直径的O与CE相切于点D,AD∥OC,点F为OC与O的交点,连接AF.(1)求证:CB是O的切线;(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
题目详情
如图,在△BCE中,点A是边BE上一点,以AB为直径的 O与CE相切于点D,AD∥OC,点F为OC与 O的交点,连接AF.
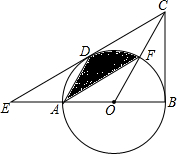
(1)求证:CB是 O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.

(1)求证:CB是 O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
▼优质解答
答案和解析
(1)证明:连接OD,与AF相交于点G,
∵CE与 O相切于点D,
∴OD⊥CE,
∴∠CDO=90°,
∵AD∥OC,
∴∠ADO=∠1,∠DAO=∠2,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠1=∠2,
在△CDO和△CBO中,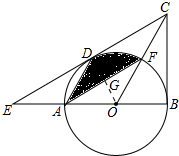
,
∴△CDO≌△CBO,
∴∠CBO=∠CDO=90°,
∴CB是 O的切线.
(2)由(1)可知∠3=∠BCO,∠1=∠2,
∵∠ECB=60°,
∴∠3=
∠ECB=30°,
∴∠1=∠2=60°,
∴∠4=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴AD=OD=OF,∵∠1=∠ADO,
在△ADG和△FOG中,
,
∴△ADG≌△FOG,
∴S△ADG=S△FOG,
∵AB=6,
∴ O的半径r=3,
∴S阴=S扇形ODF=
=
π.
∵CE与 O相切于点D,
∴OD⊥CE,
∴∠CDO=90°,
∵AD∥OC,
∴∠ADO=∠1,∠DAO=∠2,
∵OA=OD,
∴∠ADO=∠DAO,
∴∠1=∠2,
在△CDO和△CBO中,

|
∴△CDO≌△CBO,
∴∠CBO=∠CDO=90°,
∴CB是 O的切线.
(2)由(1)可知∠3=∠BCO,∠1=∠2,
∵∠ECB=60°,
∴∠3=
| 1 |
| 2 |
∴∠1=∠2=60°,
∴∠4=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴AD=OD=OF,∵∠1=∠ADO,
在△ADG和△FOG中,
|
∴△ADG≌△FOG,
∴S△ADG=S△FOG,
∵AB=6,
∴ O的半径r=3,
∴S阴=S扇形ODF=
| 60π•32 |
| 360 |
| 3 |
| 2 |
看了 如图,在△BCE中,点A是边...的网友还看了以下:
在一定条件下,至于密闭容器中的下列各组物质充分反应,在冷却到常温,密闭容器中的气态物质属于纯净物的是 2020-03-31 …
设a,b,c均为正实数,且3的a次方=4的b次方=6的c次方,证明1/c=1/a+1/2b 2020-05-15 …
根据下列条件,判断三角形abc与三角形a'b'c'是否相似,并说明理由,(1)∠a=100°,ab 2020-05-16 …
平移抛物线y=二分之一x的平方,使顶点坐标为如果将抛物线y=ax的平方+bx+c向右平移2个单位, 2020-05-16 …
复数-根号3+i的三角形式可以表示为A.2(cosπ/6+isinπ/6)B.2(cos11π/6 2020-06-02 …
内容:规划IP地址学校计算机中心有6个局域网每个局域网最多有30台主机求实验结果、实验步骤:1)申 2020-06-12 …
求解Orz在三角形ABC中,内角A、B、C所对的边分别为a,b,c,已知a-c=根号6/6,sin 2020-06-17 …
解答4元1次方程我疯了居然解半天解不出来-8a+4b-2c+d=4412a-4b+c=06a+2b 2020-06-19 …
a、了、c满足:3的a次方乖于4的b次方乖于6的c次方,求2/c-1/b=2/a,这个题怎么解啊? 2020-06-20 …
排列组合忘光了求9个人6个参加节目一共有多少组合C(9,6)求9个人6个参加节目一共有多少组合C( 2020-06-25 …