早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.(1)求证:AC是O的切线;(2)若OB=10,CD=8,求CE的长.
题目详情
如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
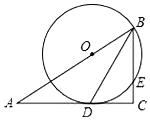
(1)求证:AC是 O的切线;
(2)若OB=10,CD=8,求CE的长.

(1)求证:AC是 O的切线;
(2)若OB=10,CD=8,求CE的长.
▼优质解答
答案和解析
(1)证明:连接OD,如图,
∵BD为∠ABC平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,
∴∠ODA=90°,
∴AC是 O的切线;
(2) 过O作OG⊥BC,连接OE,
则四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∵OG⊥BE,OB=OE,
∴BE=2BG=12.
解得:BE=12,
∵AC是 O的切线,
∴CD2=CE•CB,
即82=CE(CE+12),
解得:CE=4或CE=-16(舍去),
即CE的长为4.
∵BD为∠ABC平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,

∴∠ODA=90°,
∴AC是 O的切线;
(2) 过O作OG⊥BC,连接OE,
则四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∵OG⊥BE,OB=OE,
∴BE=2BG=12.
解得:BE=12,
∵AC是 O的切线,
∴CD2=CE•CB,
即82=CE(CE+12),
解得:CE=4或CE=-16(舍去),
即CE的长为4.
看了 如图,在Rt△ABC中,∠C...的网友还看了以下:
设A是n阶实对称矩阵,A^2=A,证明存在正交矩阵.设A是n阶实对称矩阵,A^2=A,证明存在正交 2020-05-15 …
r(A*A^T)=r(A^T*A)=r(A)证明方程AX=0与A^TAX=0同解AX=0显然有A^ 2020-06-10 …
如图,O1与O2相交于P、Q两点,过P点作两圆的割线分别交于O1与O2于A、B,过A、B分别作两圆 2020-06-15 …
对任意列向量a=[a1a2.an]^T都有Aa=0,求证:A=0设矩阵A属于M(m,n),对任意列 2020-07-09 …
数列an满足递推式(a(n+2))*an-(a(n+1))^2=(t^n)*(t-1),a1=1, 2020-08-01 …
我们把定义在R上,且满足f(x+T)=af(x)(其中常数a,T满足a≠1,a≠0,T≠0)的函数 2020-08-02 …
1.已知a*x^3=b*y^3=c*z^3且1/x+1/y+1/z=1求证(a*x^2+b*y^2+ 2020-10-31 …
关于A=0的证明设A是n阶实对称矩阵,且A²=0证明A=0.其中一种证明方法是这样的:由A(T)A= 2020-11-03 …
令T是一棵顶点数为偶数的树,证明:T恰有一个生成子图使得其中每个顶点的度均为奇数.请用图论的方法证明 2020-11-18 …
证明分块矩阵可逆求证设A,B,C是复数域上的n阶矩阵,且T=[AB;0C]是2n阶矩阵,证明T是可逆 2020-12-31 …