早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC时(1)若CE⊥BD于E,①∠ECD=°;②求证:BD=2EC;(2)如图,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90&d
题目详情
如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC时
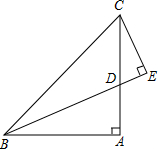
(1)若CE⊥BD于E,
①∠ECD=___°;
②求证:BD=2EC;
(2)如图,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FPC与∠PFC的角平分线的交点.当点P运动时,点Q是否一定在射线BD上?若在,请证明,若不在;请说明理由.

(1)若CE⊥BD于E,
①∠ECD=___°;
②求证:BD=2EC;
(2)如图,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FPC与∠PFC的角平分线的交点.当点P运动时,点Q是否一定在射线BD上?若在,请证明,若不在;请说明理由.
▼优质解答
答案和解析
(1)①∵∠BAC=90°,CE⊥BD,∠ADB=∠CDE,
∴∠ABD=∠ECD,
又∵∠BAC=90°,AB=AC,BD平分∠ABC,
∴∠ABD=22.5°,
∴∠ECD=22.5°;
故答案为:22.5.
②如图,延长CE交BA的延长线于点G,
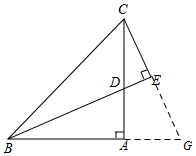
∵BD平分∠ABC,CE⊥BD,
∴CE=GE,
在△ABD与△ACG中,
,
∴△ABD≌△ACG(AAS),
∴BD=CG=2CE;
(2)点Q一定在射线BD上,
理由:如图,连接CQ,过点Q作QM⊥BP于M,作QN⊥BC于N,
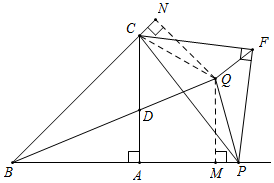
∵QF为∠PFC的角平分线,△CPF为等腰直角三角形,
∴QF为PC的垂直平分线,
∴PQ=QC,
∵Q为∠FPC与∠PFC的角平分线的交点,
∴CQ平分∠FCP,
∵△CPF为等腰直角三角形,
∴∠FCP=∠FPC=45°,
∴∠QCP=∠QPC=22.5°,
∴△PQC中,∠PQC=135°,
∵在四边形QNBM中,QM⊥BP,QN⊥BC,∠ABC=45°,
∴∠MQN=135°,
∴∠MQN=∠PQC,
∴∠NQC=∠MQP,
又∵QC=QP,QM⊥BP,QN⊥BC,
∴△QPM≌△QCN(AAS),
∴QM=QN,
又∵QM⊥BP,QN⊥BC,
∴点Q一定在射线BD上.
∴∠ABD=∠ECD,
又∵∠BAC=90°,AB=AC,BD平分∠ABC,
∴∠ABD=22.5°,
∴∠ECD=22.5°;
故答案为:22.5.
②如图,延长CE交BA的延长线于点G,

∵BD平分∠ABC,CE⊥BD,
∴CE=GE,
在△ABD与△ACG中,
|
∴△ABD≌△ACG(AAS),
∴BD=CG=2CE;
(2)点Q一定在射线BD上,
理由:如图,连接CQ,过点Q作QM⊥BP于M,作QN⊥BC于N,

∵QF为∠PFC的角平分线,△CPF为等腰直角三角形,
∴QF为PC的垂直平分线,
∴PQ=QC,
∵Q为∠FPC与∠PFC的角平分线的交点,
∴CQ平分∠FCP,
∵△CPF为等腰直角三角形,
∴∠FCP=∠FPC=45°,
∴∠QCP=∠QPC=22.5°,
∴△PQC中,∠PQC=135°,
∵在四边形QNBM中,QM⊥BP,QN⊥BC,∠ABC=45°,
∴∠MQN=135°,
∴∠MQN=∠PQC,
∴∠NQC=∠MQP,
又∵QC=QP,QM⊥BP,QN⊥BC,
∴△QPM≌△QCN(AAS),
∴QM=QN,
又∵QM⊥BP,QN⊥BC,
∴点Q一定在射线BD上.
看了 如图,在△ABC中,∠BAC...的网友还看了以下:
已知点P在四边形ABCD所在平面外,如果把两条异面直线看成一对,那么P与四边形ABCD的四个顶点的 2020-05-01 …
一直p为曲线c上任一点,若p到点F(1/2,0)的距离与p带直线x=-1/2距离相等求曲线方程试问 2020-05-14 …
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列 2020-05-16 …
如图所示,点P是正方形ABCD的对角线BD上一点,PE⊥BC于E,PF⊥CD于F,连接EF,给出下 2020-06-17 …
如图所示,P为固定闭合回路的一段导体的横截面,若使一对异性磁极相对P运动,并让P始终处于磁场中,则 2020-07-22 …
已知平面上一点M(5,0),若直线上存在点P使|PM|=4,则称该直线为“切割型直线”,下列直线中 2020-07-26 …
三棱锥P-ABC中中,顶点P中在底面ABC中内的射影为O中,若(1)三条侧棱与底面所成的角相等,( 2020-07-30 …
三棱锥V-ABC中,侧棱VA,VB,VC两两垂直,P是底面ABC内一点且点P到三个侧面的距离分别是 2020-07-30 …
如图,在平面直角坐标系中,已知△ABC与△DEF关于点P中心对称(1)求出点P的坐标;(2)将△DE 2020-12-25 …
一个物体做自由落体运动,落地式的速度是经过空中P点是速度的二倍,一直P点离地面的高度为15m.g取1 2021-01-22 …