早教吧作业答案频道 -->数学-->
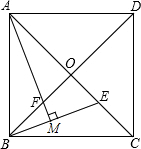
如图,正方形ABCD的边长为22,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为.
题目详情
如图,正方形ABCD的边长为2
,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F,则FM的长为___.
| | 2 |

▼优质解答
答案和解析
 ∵正方形ABCD
∵正方形ABCD
∴AO=BO,∠AOF=∠BOE=90°
∵AM⊥BE,∠AFO=∠BFM
∴∠FAO=∠EBO
在△AFO和△BEO中
∴△AFO≌△BEO(ASA)
∴FO=EO
∵正方形ABCD的边长为2
,E是OC的中点
∴FO=EO=1=BF,BO=2
∴直角三角形BOE中,BE=
=
由∠FBM=∠EBO,∠FMB=∠EOB,可得△BFM∽△BEO
∴
=
,即
=
∴FM=
故答案为:
 ∵正方形ABCD
∵正方形ABCD∴AO=BO,∠AOF=∠BOE=90°
∵AM⊥BE,∠AFO=∠BFM
∴∠FAO=∠EBO
在△AFO和△BEO中
|
∴△AFO≌△BEO(ASA)
∴FO=EO
∵正方形ABCD的边长为2
| 2 |
∴FO=EO=1=BF,BO=2
∴直角三角形BOE中,BE=
| 12+22 |
| 5 |
由∠FBM=∠EBO,∠FMB=∠EOB,可得△BFM∽△BEO
∴
| FM |
| EO |
| BF |
| BE |
| FM |
| 1 |
| 1 | ||
|
∴FM=
| ||
| 5 |
故答案为:
| ||
| 5 |
看了 如图,正方形ABCD的边长为...的网友还看了以下:
(2014•烟台)在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC, 2020-06-12 …
我想用几何画板画出一个动点运动后 另一个点随它以2倍的速度运动 怎么画?这是具体题目在射线A上取一 2020-06-27 …
把一张矩形ABCD纸片折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上)折痕分别为BH 2020-07-10 …
把一张矩形纸片ABCD按如图所示折叠,使A点与点E重合,点C与点F重合(E,F两点均在BD上)折痕 2020-07-10 …
如图,已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上,且AC=60c,BC= 2020-07-14 …
如图,已知∠ABC=90°,AB=BC.直线l与以BC为直径的圆O相切于点C.点F是圆O上异于B、 2020-07-22 …
把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折 2020-07-30 …
如图,在平面直角坐标系中,抛物线W1:y=-x2+6x-5与x轴交于A、B两点,点C是该抛物线的顶 2020-08-02 …
如图是放在地面上的一个长方体盒子,其中AB=9,BB′=5,B′C′=6,在线段AB的三等分点E( 2020-08-02 …
在正方形ABCD中,动点E、F分别从D、C两点同时出发,以相同的速度在直线DC、CB上移动(1)如图 2020-11-02 …