早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,抛物线W1:y=-x2+6x-5与x轴交于A、B两点,点C是该抛物线的顶点.(1)若抛物线W1与抛物线W2关于直线x=-1对称,其中,点C与点F,点E与点B,点D与点A是对应点,求抛
题目详情
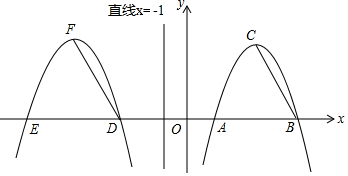
如图,在平面直角坐标系中,抛物线W1:y=-x2+6x-5与x轴交于A、B两点,点C是该抛物线的顶点.
(1)若抛物线W1与抛物线W2关于直线x=-1对称,其中,点C与点F,点E与点B,点D与点A是对应点,求抛物线W2的表达式.
(2)连接BC,在直线x=-1上找一点H,使得△BCH周长最小,并求出点H的坐标.
(3)连接FD,点P是直线x=-1上一点,点Q是抛物线W1上一点,若以点D、F、P、Q为顶点的四边形是平行四边形,请求出符合条件的点Q的坐标.
(1)若抛物线W1与抛物线W2关于直线x=-1对称,其中,点C与点F,点E与点B,点D与点A是对应点,求抛物线W2的表达式.
(2)连接BC,在直线x=-1上找一点H,使得△BCH周长最小,并求出点H的坐标.
(3)连接FD,点P是直线x=-1上一点,点Q是抛物线W1上一点,若以点D、F、P、Q为顶点的四边形是平行四边形,请求出符合条件的点Q的坐标.

▼优质解答
答案和解析
(1)令y=0得:0=-x2+6x-5,解得x=1或x=5,
∴A(1,0),B(5,0).
∵点E与段B关于x=-1对称,
∴点E(-7,0).
∴AE=8.
∴W2可由W1向右平移8个单位得到.
∴抛物线W2的表达式为y=-(x+8)2+6(x+8)-5,即y=-x2-10x-21.
(2)如图1所示:连结BF交x=-1与H.
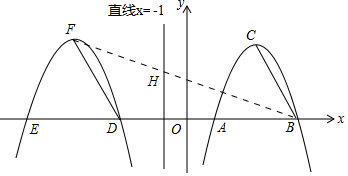
∵y=-x2+6x-5=-(x-3)2+4,
∴C(3,4).
∵点F与点C关于x=-1对称,
∴FH=CH,F(-5,4).
∴当点F、H、B在一条直线上时,HC+BH有最小值,即△BCH的周长最小.
设BF的解析式为y=kx+b,将点B和点F的坐标代入得:
,解得:k=-
,b=2.
∴直线BF的解析式为y=-
x+2.
当x=-1时,y=
.
∴H(-1,
).
(3)当DP为平行四边形的对角线时,设点P的坐标为(-1,a),Q(x,y).
∵平行四边形的对角线互相平分,
∴
=
,
=
,
∴x=1,y=a-4.
∴Q(1,a-4).
将点Q的坐标代入W1的解析式得:a-4=-1+6-5,解得a=4.
∴Q(1,0).
当DP为平行四边形的边时.设点P的坐标为(-1,a).
∵平行四边形的对边平行且相等,
∴PQ可看作由DF平移得到.
∴点Q的坐标为(-1-2,a+4).
将点Q的坐标代入W1的解析式得:a+4=-9+6×(-3)-5,解得a=-36.
∴Q(-3,-32).
综上所述,点Q的坐标为(1,0)或(-3,-32)时,以点D、F、P、Q为顶点的四边形是平行四边形.
∴A(1,0),B(5,0).
∵点E与段B关于x=-1对称,
∴点E(-7,0).
∴AE=8.
∴W2可由W1向右平移8个单位得到.
∴抛物线W2的表达式为y=-(x+8)2+6(x+8)-5,即y=-x2-10x-21.
(2)如图1所示:连结BF交x=-1与H.

∵y=-x2+6x-5=-(x-3)2+4,
∴C(3,4).
∵点F与点C关于x=-1对称,
∴FH=CH,F(-5,4).
∴当点F、H、B在一条直线上时,HC+BH有最小值,即△BCH的周长最小.
设BF的解析式为y=kx+b,将点B和点F的坐标代入得:
|
| 2 |
| 5 |
∴直线BF的解析式为y=-
| 2 |
| 5 |
当x=-1时,y=
| 12 |
| 5 |
∴H(-1,
| 12 |
| 5 |
(3)当DP为平行四边形的对角线时,设点P的坐标为(-1,a),Q(x,y).
∵平行四边形的对角线互相平分,
∴
| x-5 |
| 2 |
| -3-1 |
| 2 |
| 0+a |
| 2 |
| 4+y |
| 2 |
∴x=1,y=a-4.
∴Q(1,a-4).
将点Q的坐标代入W1的解析式得:a-4=-1+6-5,解得a=4.
∴Q(1,0).
当DP为平行四边形的边时.设点P的坐标为(-1,a).
∵平行四边形的对边平行且相等,
∴PQ可看作由DF平移得到.
∴点Q的坐标为(-1-2,a+4).
将点Q的坐标代入W1的解析式得:a+4=-9+6×(-3)-5,解得a=-36.
∴Q(-3,-32).
综上所述,点Q的坐标为(1,0)或(-3,-32)时,以点D、F、P、Q为顶点的四边形是平行四边形.
看了 如图,在平面直角坐标系中,抛...的网友还看了以下:
根据一元二次方程的ax²+bx+c=0的求根公式,回答问题x=-b±√b²-4ac/2a 可求x 2020-05-16 …
已知抛物线y=1/2x^2+x-5/2. (1)用配方法求它的顶点坐标和对称轴 (2)若该抛物线与 2020-05-16 …
证明无论a取任何实数值,抛物线y=x2+(a+1)x+0.5a+0.25是通过一个定点而且这些抛物 2020-06-03 …
以点A(4,-3)为直角顶点的Rt△OAB中,|AB|=2|OA|且点B纵坐标大于0.(1)求向量 2020-06-21 …
已知抛物线y=-1/2(x-2)².(1)求它的顶点A及与y轴交点B的坐标已知抛物线y=-1/2( 2020-06-29 …
1.有理数X1、X2表示在数轴上得到点A1、A2,我们就把X1、X2叫做A1、A2的一维坐标.一般 2020-08-03 …
有理数x1,x2表示数轴上得到点A1,A2,我们就把x1,x2叫做A1,A2的一维坐标.一般地称| 2020-08-03 …
如图(1),抛物线W1:y=-x2+4x与x轴的正半轴交于点B,顶点为A,抛物线W2与W1关于x轴对 2020-10-31 …
y=x2+2x-3,开口方向,对称轴,顶点坐标 2020-11-04 …
若x1满足2x+2^x=5,x2满足2x+2log2(x+1)=5,求x1+x2=多少?2X+2^x 2020-11-19 …