早教吧作业答案频道 -->数学-->
作图与证明:如图,已知O和O上的一点A,请完成下列任务:(1)作O的内接正六边形ABCDEF;(2)连接BF,CE,判断四边形BCEF的形状并加以证明.
题目详情
作图与证明:
如图,已知 O和 O上的一点A,请完成下列任务:
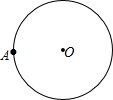
(1)作 O的内接正六边形ABCDEF;
(2)连接BF,CE,判断四边形BCEF的形状并加以证明.
如图,已知 O和 O上的一点A,请完成下列任务:

(1)作 O的内接正六边形ABCDEF;
(2)连接BF,CE,判断四边形BCEF的形状并加以证明.
▼优质解答
答案和解析
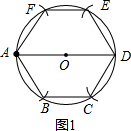 (1)如图1,首先作直径AD,然后分别以A,D为圆心,OA长为半径画弧,分别交 O于点B,F,C,E,连接AB,BC,CD,DE,EF,AF,
(1)如图1,首先作直径AD,然后分别以A,D为圆心,OA长为半径画弧,分别交 O于点B,F,C,E,连接AB,BC,CD,DE,EF,AF,
则正六边形ABCDEF即为 O所求;
(2)四边形BCEF是矩形.
理由:如图2,连接OE,
∵六边形ABCDEF是正六边形,
∴AB=AF=DE=DC,FE=BC,
∴
=
=
=
,
∴
=
,
∴BF=CE,
∴四边形BCEF是平行四边形,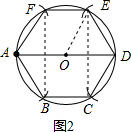
∵∠EOD=
=60°,OE=OD,
∴△EOD是等边三角形,
∴∠OED=∠ODE=60°,
∴∠EDC=∠FED=2∠ODE=120°,
∵DE=DC,
∴∠DEC=∠DCE=30°,
∴∠CEF=∠DEF-∠CED=90°,
∴四边形BCEF是矩形.
 (1)如图1,首先作直径AD,然后分别以A,D为圆心,OA长为半径画弧,分别交 O于点B,F,C,E,连接AB,BC,CD,DE,EF,AF,
(1)如图1,首先作直径AD,然后分别以A,D为圆心,OA长为半径画弧,分别交 O于点B,F,C,E,连接AB,BC,CD,DE,EF,AF,则正六边形ABCDEF即为 O所求;
(2)四边形BCEF是矩形.
理由:如图2,连接OE,
∵六边形ABCDEF是正六边形,
∴AB=AF=DE=DC,FE=BC,
∴
 |
| AB |
 |
| AF |
 |
| DE |
 |
| DC |
∴
 |
| BF |
 |
| CE |
∴BF=CE,
∴四边形BCEF是平行四边形,

∵∠EOD=
| 360° |
| 6 |
∴△EOD是等边三角形,
∴∠OED=∠ODE=60°,
∴∠EDC=∠FED=2∠ODE=120°,
∵DE=DC,
∴∠DEC=∠DCE=30°,
∴∠CEF=∠DEF-∠CED=90°,
∴四边形BCEF是矩形.
看了 作图与证明:如图,已知O和O...的网友还看了以下:
线性代数 方阵的行列式的性质:请证明方阵的行列式的性质:A,B为方阵,则AB乘积的行列式等于A的行 2020-05-15 …
如图,⊙O的直径为AB,⊙O1过点O,且与⊙O内切于点B.C为⊙O上的点,OC与⊙O1交于点D,且 2020-06-16 …
几何证明圆O为三角形abc的外接圆,圆O1分别与AB,AC相切于点D,E,与圆O内切于点P.求证: 2020-07-22 …
凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点 2020-07-25 …
已知圆O和圆O上的一点A1作圆O的内接正方形ABCD和内接正六边形AEFCGH2在1题所做的图中, 2020-07-26 …
如图,在▱ABCD中,∠A的平分线分别与BC及DC的延长线交于点E、F,点O、O1分别为△CEF、 2020-07-30 …
已知⊙O内接△ABC,⊙Q切AB,AC于E,F且与⊙O内切.试证:EF中点P是△ABC之内心. 2020-07-31 …
已知⊙O内接△ABC,⊙Q切AB,AC于E,F且与⊙O内切.试证:EF中点P是△ABC之内心. 2020-07-31 …
如图,M是以AB为直径的⊙O内的一点,AM,BM的延长线分别与圆O交于点C,D,过点M作MN⊥AB于 2020-11-01 …
已知⊙O与⊙O′内切于点A,⊙O的弦BC与⊙O′切于点D,AB、AC与⊙O′分别交于点E、F,AG、 2020-12-01 …