早教吧作业答案频道 -->数学-->
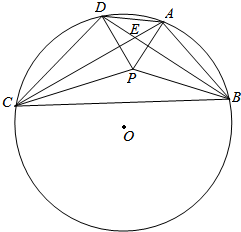
凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.
题目详情
凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.

▼优质解答
答案和解析
 证明:引理:圆O内有一点K,A1B1、A2B2、A3B3、A4B4是过K的圆O的弦,
证明:引理:圆O内有一点K,A1B1、A2B2、A3B3、A4B4是过K的圆O的弦,
若A1A2∩A3A4=M,B1B2∩B3B4=N,则K,M,N三点共线.
引理的证明:在圆O所在的实射影平面内考虑这样一个射影变换,
它把圆O变为圆,把K为圆心,K的像记为k′等等,
则由圆K′的对称性,A1′A2′与B1′B2′关于K′中心对称,A3′A4′与B3′B4′关于K′中心对称,
故M′与N′关于K′中心对称,从而K′、M′、N′三点共线,
由射影变换性质,得原来K、M、N三点共线.
下面回到本题:
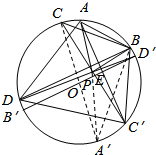
延长AP、BP、CP、DP分别交 O于A′、B′、C′、D′,
连结A′C′、B′D′、A‘B、BC’,
则∠A′C′B+∠CA′B=∠A′AB+∠C′CB=90°,
∴∠A′BC′=90°,A′C′为直径,同理B′D′为直径,
∵A不与D、D重合,A′C′不与B′D′重合,∴A′C′∩B′D′=O,
在引理中,令K=P,A1=A,A2=C,B1=B,B2=D,即得到O、P、E三点共线,
∴O、P、E共线.
 证明:引理:圆O内有一点K,A1B1、A2B2、A3B3、A4B4是过K的圆O的弦,
证明:引理:圆O内有一点K,A1B1、A2B2、A3B3、A4B4是过K的圆O的弦,若A1A2∩A3A4=M,B1B2∩B3B4=N,则K,M,N三点共线.
引理的证明:在圆O所在的实射影平面内考虑这样一个射影变换,
它把圆O变为圆,把K为圆心,K的像记为k′等等,
则由圆K′的对称性,A1′A2′与B1′B2′关于K′中心对称,A3′A4′与B3′B4′关于K′中心对称,
故M′与N′关于K′中心对称,从而K′、M′、N′三点共线,
由射影变换性质,得原来K、M、N三点共线.
下面回到本题:
延长AP、BP、CP、DP分别交 O于A′、B′、C′、D′,
连结A′C′、B′D′、A‘B、BC’,
则∠A′C′B+∠CA′B=∠A′AB+∠C′CB=90°,
∴∠A′BC′=90°,A′C′为直径,同理B′D′为直径,
∵A不与D、D重合,A′C′不与B′D′重合,∴A′C′∩B′D′=O,
在引理中,令K=P,A1=A,A2=C,B1=B,B2=D,即得到O、P、E三点共线,
∴O、P、E共线.
看了 凸四边形ABCD的外接圆的圆...的网友还看了以下:
we will wait here until 9 o 'clock tomorrow morni 2020-05-16 …
三角形ABC内接于圆O,D是圆上一点,连接B、D,C、D,AC与BD交与点E,请找出图中相似△,如 2020-06-04 …
判断下列各组单词括号内部分发音是否相同.h(o)td(o)g()cl(o)ckc(o)ffee() 2020-06-26 …
进制换算(213)D=()B=()H=()O(69.625)D=()D=()B=()O(127)D 2020-07-19 …
如图所示,两根平行放置的金属导轨COD、C′O′D′,导轨OC,O′C′部分粗糙,处在同一水平面内 2020-07-19 …
O,I分别是锐角三角形ABC的外心,内心.O',I'分别是O,I关于BC的对称点.已知A、B、O' 2020-07-30 …
如图:⊙O和⊙O'内切于P半径OA和OB切⊙O'于C、D连O'C和O'D如果两圆半径分别为9和3则 2020-07-31 …
(过程)已知等边三角形ABC内接于圆O,D为直线AB上一点已知等边三角形ABC内接于圆O,D为直线 2020-08-03 …
通过计算前三个算式,找出规律后把其他算式补充完整,再用计算器检验.2.1×O.9÷0.1=3.21× 2021-01-01 …
写出下列单词的比较级和最高级(6)bOring(8)|ong(9)o|d(12)inteSestin 2021-01-30 …