如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC=FG；②S△FAB：S四边形CEFG=1：2；③∠ABC

Question

如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：
①AC=FG；②S_△FAB：S_{四边形CEFG}=1：2；③∠ABC=∠ABF；④AD²=FQ•AC，
其中正确的结论的个数是（　　）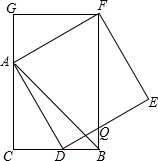

A. 1

B. 2

C. 3

D. 4

Answer 1

∵四边形ADEF为正方形，
∴∠FAD=90°，AD=AF=EF，
∴∠CAD+∠FAG=90°，
∵FG⊥CA，
∴∠C=90°=∠ACB，
∴∠CAD=∠AFG，
在△FGA和△ACD中，

∠G=∠C

∠AFG=∠CAD

AF=AD

，
∴△FGA≌△ACD（AAS），
∴AC=FG，①正确；
∵BC=AC，
∴FG=BC，
∵∠ACB=90°，FG⊥CA，
∴FG∥BC，
∴四边形CBFG是矩形，
∴∠CBF=90°，S_△FAB=(1)/(2)FB•FG=(1)/(2)S_{四边形CEFG}，②正确；
∵CA=CB，∠C=∠CBF=90°，
∴∠ABC=∠ABF=45°，③正确；
∵∠FQE=∠DQB=∠ADC，∠E=∠C=90°，
∴△ACD∽△FEQ，
∴AC：AD=FE：FQ，
∴AD•FE=AD²=FQ•AC，④正确；
故选：D．