△ABC中，AD⊥BC交BC于D，AE平分∠BAC交BC于E，F为BC延长线上一点，FG⊥AE交AD的延长线于G，AC的延长线交FG于H，连接BG，下列结论：①∠DAE=∠F；②∠AGH=∠BAE+∠ACB；③S△AEB：S△AEC=AB：CA；④∠ABC

Question

△ABC中，AD⊥BC交BC于D，AE平分∠BAC交BC于E，F为BC延长线上一点，FG⊥AE交AD的延长线于G，AC的延长线交FG于H，连接BG，下列结论：
①∠DAE=∠F；
②∠AGH=∠BAE+∠ACB；
③S_△AEB：S_△AEC=AB：CA；
④∠ABC+∠ACB=2∠AHG，
其中正确的结论有（　　）个．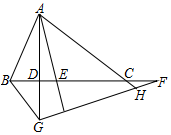

A. 1

B. 2

C. 3

D. 4

Answer 1

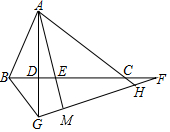如图，①∵AD⊥BC，FG⊥AE，
∴∠ADE=∠AMF=90°，
∵∠AED=∠MEF，
∴∠DAE=∠F；故①正确；
②∵∠DAE=∠F，∠FDG=∠FME=90°，
∴∠AGH=∠MEF，
∵AE平分∠BAC交BC于E，
∴∠BAE=∠CAE，
∵∠MEF=∠CAE+∠ACB，
∴∠AGH=∠CAE+∠ACB，
∴∠AGH=∠BAE+∠ACB；故②正确；
③∵AE平分∠BAC交BC于E，
∴(AB)/(AC)=(BE)/(CE)，
∵S_△AEB：S_△AEC=((1)/(2)BE•AD)/((1)/(2)CE•AD)=(BE)/(CE)，
∴S_△AEB：S_△AEC=AB：CA；故③正确；
④∵∠AMH=90°，
∴∠AHG=90°-∠CAE=90°-(1)/(2)∠BAC，
∵∠BAC=180°-∠ABC-∠ACB，
∴∠AHG=90°-(1)/(2)（180°-∠ABC-∠ACB）=(1)/(2)（∠ABC+∠ACB），
即∠ABC+∠ACB=2∠AHG；故④正确．
故选D．