早教吧作业答案频道 -->数学-->
如图,在矩形ABCD中,AB=1,BC=2,点E是AD边上一动点(不与点A,D重合),过A、E、C三点的O交AB延长线于点F,连接CE、CF.(1)求证:△DEC∽△BFC;(2)设DE的长为x,△AEF的面积为y.①求y
题目详情
如图,在矩形ABCD中,AB=1,BC=2,点E是AD边上一动点(不与点A,D重合 ),过A、E、C三点的 O交AB延长线于点F,连接CE、CF.
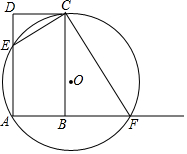
(1)求证:△DEC∽△BFC;
(2)设DE的长为x,△AEF的面积为y.
①求y关于x的函数关系式,并求出当x为何值时,y有最大值;
②连接AC,若△ACF为等腰三角形,求x的值.

(1)求证:△DEC∽△BFC;
(2)设DE的长为x,△AEF的面积为y.
①求y关于x的函数关系式,并求出当x为何值时,y有最大值;
②连接AC,若△ACF为等腰三角形,求x的值.
▼优质解答
答案和解析
(1)证明:如图1中,连接EF.
∵四边形ABCD是矩形,
∴AB=CD=1,AD=BC=2,∠A=∠D=∠DCB=∠ABC=∠CBF=90°,
∴EF是 O直径,
∴∠ECF=90°,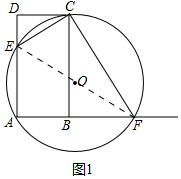
∴∠DCB=∠ECF,
∴∠DCE=∠BCF,∵∠D=∠CBF,
∴△DEC∽△BFC.
(2)①∵△DEC∽△BFC,
∴
=
,
∴
=
,
∴BF=2x,AF=1+2x,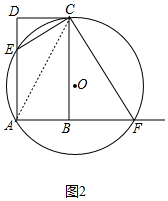
∴y=
•AE•AF=
(2-x)(1+2x)=-x2+
x+1=-(x-
)2+
,
∵-1<0,
∴当x=
时,y有最大值.
②如图2中,a、当AC=AF=
时,
∵BF=2x=
-1,
∴x=
.
b、当CA=CF时,易知AB=BF=1,
∴2x=1,
∴x=
.
c、当FC=FA时,则有(2x)2+22=(1+2x)2,
解得x=
,
综上所述,△ACF为等腰三角形,x的值为
或
或
.
∵四边形ABCD是矩形,
∴AB=CD=1,AD=BC=2,∠A=∠D=∠DCB=∠ABC=∠CBF=90°,
∴EF是 O直径,
∴∠ECF=90°,

∴∠DCB=∠ECF,
∴∠DCE=∠BCF,∵∠D=∠CBF,
∴△DEC∽△BFC.
(2)①∵△DEC∽△BFC,
∴
| DE |
| BF |
| CD |
| CB |
∴
| x |
| BF |
| 1 |
| 2 |
∴BF=2x,AF=1+2x,

∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 25 |
| 16 |
∵-1<0,
∴当x=
| 3 |
| 4 |
②如图2中,a、当AC=AF=
| 5 |
∵BF=2x=
| 5 |
∴x=
| ||
| 2 |
b、当CA=CF时,易知AB=BF=1,
∴2x=1,
∴x=
| 1 |
| 2 |
c、当FC=FA时,则有(2x)2+22=(1+2x)2,
解得x=
| 3 |
| 4 |
综上所述,△ACF为等腰三角形,x的值为
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
看了 如图,在矩形ABCD中,AB...的网友还看了以下:
大家帮我看看这个一阶微分方程Af(x)+b(f'(x))^2=d求f(x) 2020-04-26 …
如图,四边形ABCD是平行四边形,点E、F分别为AD、BC边上的点,且AE=CF求证:四边形BED 2020-05-16 …
-『』矩形abcd沿着AE折叠,使D落在BC边上的F点,如果AD=10,AB=6.求三角形AFE的 2020-05-23 …
已知:如图,将长方形ABCD沿着AE折叠,使得点D落在BC边上点F处,AB=8,AD=10,求EC 2020-07-26 …
已知函数f(x)=根号3sin2x-2sin平方x(1)若点p(1,-根号3)在角α的终边上,求f 2020-07-30 …
如图,已知抛物线与x轴相交于A,B两点,与y轴相交于点C(0,-3),且顶点D的坐标为(1,-4) 2020-08-01 …
如图所示,圆i是R他△ABC的内切圆,角C=90°,圆i和三边分别相切于点D,E,F.如图,圆I是 2020-08-01 …
1.如下图,在三角形ABC中,BD=2DC,AE=2ED,FC=7,求AF.(注:D在BC边上;F在 2020-11-03 …
已知,△ABC是等边三角形,点D为直线BC上一点(端点B、C除外),以AD为边作等边△ADF,连接C 2020-12-10 …
、已知:▱ABCD中,E是BA边延长线上一点,CE交对角线DB于点G,交AD边于点F.求证:1、已知 2020-12-25 …