早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,直线y=kx(k≠0)经过点(a,3a)(a>0),线段BC的两个端点分别在x轴与直线y=kx上(点B、C均与原点O不重合)滑动,且BC=2,分
题目详情
如图,在平面直角坐标系中,直线y=kx(k≠0)经过点(a,
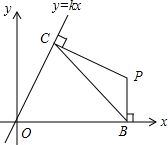
a)(a>0),线段BC的两个端点分别在x轴与直线y=kx上(点B、C均与原点O不重合)滑动,且BC=2,分别作BP⊥x轴,CP⊥直线y=kx,交点为P.经探究,在整个滑动过程中,P、O两点间的距离为定值___.
| | 3 |

▼优质解答
答案和解析
∵直线y=kx(k≠0)经过点(a,
a)(a>0),
∴
a=ka,
∴k=
,
∴∠BOC=60°,
又由题意可知∠PCO=∠PBO=90°,
∴∠PCO+∠PBO=180°,
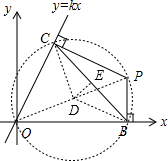
∴O、B、P、C四点共圆,OP为直径,
如图,设圆心为D,分别连接CD和BD,过D作DE⊥BC于点E,
则BE=
BC=1,
∵∠BDC=2∠BOC=120°,
∴∠BDE=60°,
∴DE=
BD,
在Rt△BDE中,由勾股定理可得BD2=DE2+BE2,
即BD2=
BD2+1,
解得BD=
,
∴OP=2BD=
,
故答案为:
.

∵直线y=kx(k≠0)经过点(a,
| 3 |
∴
| 3 |
∴k=
| 3 |
∴∠BOC=60°,
又由题意可知∠PCO=∠PBO=90°,
∴∠PCO+∠PBO=180°,
∴O、B、P、C四点共圆,OP为直径,
如图,设圆心为D,分别连接CD和BD,过D作DE⊥BC于点E,
则BE=
| 1 |
| 2 |
∵∠BDC=2∠BOC=120°,
∴∠BDE=60°,
∴DE=
| 1 |
| 2 |
在Rt△BDE中,由勾股定理可得BD2=DE2+BE2,
即BD2=
| 1 |
| 4 |
解得BD=
2
| ||
| 3 |
∴OP=2BD=
4
| ||
| 3 |
故答案为:
| 4 |
| 3 |
| 3 |
看了 如图,在平面直角坐标系中,直...的网友还看了以下:
在等腰三角形ABC中,CH是底边上的高线,点P是线段CH上不与端点重合的的任意一点在等腰△ABC中 2020-05-20 …
一个滑雪运动员从85米长的山坡上匀速直线下滑初速度为1.8米每秒末速一个滑雪运动员从85米长的山坡 2020-06-05 …
在等腰三角形△ABC(C为顶点)中,CH是底边上的高线,点P是线段CH上不与端点重和的任意一点,连 2020-06-05 …
如图所示,一物块相对木板向右从板上A点滑至板上B点,木板上A、B两点间距离为5米,同时木板在地面上 2020-06-28 …
高中数学(圆锥曲线)急哟!点A(-2,0),B(2,0),动点P满足∠APB=2a,且|PA|*| 2020-06-29 …
有一在原点处与x轴相切并在第一象限的光滑曲线,P(x,y)为曲线上的任一点.设曲线在原点与P点之间 2020-07-26 …
过曲线上一点与以此点为切点的切线垂直的直线,叫做曲线在该点的法线.已知抛物线C的方程为y=ax2( 2020-07-31 …
如图所示,一滑雪运动员以一定的初速度从一平台上A点滑出,落在斜坡上的B点时,其速度方向刚好沿着斜面向 2020-10-30 …
顶点在坐标原点,开口向上的抛物线经过点,过点作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物 2020-11-04 …
(2011•威海模拟)质量m=50kg的跳台花样滑雪运动员(可看成质点),从静止开始沿斜面雪道从A点 2020-11-13 …