早教吧作业答案频道 -->数学-->
如图,已知直线y=kx(k>0)与双曲线y=8x交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点P(1,a),过点P作PQ∥y轴交直线AB于点Q.(1)直接写出k的值及点B的坐标;(2)求线
题目详情
如图,已知直线y=kx(k>0)与双曲线y=
交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点P(1,a),过点P作PQ∥y轴交直线AB于点Q.
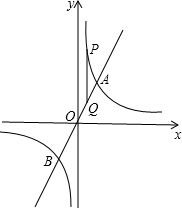
(1)直接写出k的值及点B的坐标;
(2)求线段PQ的长;
(3)如果在直线y=kx上有一点M,且满足△BPM的面积等于12,求点M的坐标.
| 8 |
| x |

(1)直接写出k的值及点B的坐标;
(2)求线段PQ的长;
(3)如果在直线y=kx上有一点M,且满足△BPM的面积等于12,求点M的坐标.
▼优质解答
答案和解析
(1)∵A在双曲线y=
交于,且A的纵坐标为4,
∴A坐标为(2,4),
代入直线y=kx,可得4=2k,解得k=2,
又A、B关于原点对称,
∴点B的坐标为(-2,-4).
(2)∵点P(1,a)在双曲线上,
∴代入y=
,可得点P的坐标为(1,8).
∵PQ∥y轴,且点Q在直线AB上,
∴可设点Q的坐标为(1,b).
代入y=2x,得点Q的坐标为(1,2).
∴PQ=6.
(3)设点M的坐标为(m,2m).
S△BPQ=
×6×3=9.
①当点M在BQ的延长线上时,S△BPM=S△BPQ+S△MPQ,12=9+
×6×(m-1),m=2.
点M的坐标为(2,4).
②当点M在QB的延长线上时,S△BPM=S△MPQ-S△BPQ,12=
×6×(1-m)-9,m=-6.
点M的坐标为(-6,-12).
综上所述:点M的坐标为(2,4),(-6,-12).
| 8 |
| x |
∴A坐标为(2,4),
代入直线y=kx,可得4=2k,解得k=2,
又A、B关于原点对称,
∴点B的坐标为(-2,-4).
(2)∵点P(1,a)在双曲线上,
∴代入y=
| 8 |
| x |
∵PQ∥y轴,且点Q在直线AB上,
∴可设点Q的坐标为(1,b).
代入y=2x,得点Q的坐标为(1,2).
∴PQ=6.
(3)设点M的坐标为(m,2m).
S△BPQ=
| 1 |
| 2 |
①当点M在BQ的延长线上时,S△BPM=S△BPQ+S△MPQ,12=9+
| 1 |
| 2 |
点M的坐标为(2,4).
②当点M在QB的延长线上时,S△BPM=S△MPQ-S△BPQ,12=
| 1 |
| 2 |
点M的坐标为(-6,-12).
综上所述:点M的坐标为(2,4),(-6,-12).
看了 如图,已知直线y=kx(k>...的网友还看了以下:
已知点p在曲线y=4/(e^X+1)上,a为曲线在点p处的切线的倾斜角,则a的取值范围是?下面是我 2020-04-11 …
已知点P(m,a)是抛物线y=a(x-1)2上的点,且点P在第一象限内.(1)求m的值;(2)过P 2020-05-14 …
几道关于直线解析几何的问题1.已知点P(0,1),过P求直线,使它夹在两条直线M:x-3y+10= 2020-05-23 …
已知点P是抛物线y^2=-4x上一点,设P到此抛物线准线距离是d1,到直线x+y-7=0的距离是已 2020-07-09 …
已知点P为抛物线y2=2x上的动点,点P在y轴上的射影为M,点A的坐标为A(72,4),则|PA| 2020-07-30 …
端点在抛物线上的定长线段的中点的轨迹是什么?已知:抛物线P:y^2=2px,线段AB的端点A、B在 2020-07-31 …
已知点P(x,y)是圆x^2+y^2-6x-4y+12=0上一点,求:.已知点P(x,y)是圆x^2 2020-10-31 …
已知点P是圆C:x^2+y^2-6x-8y+21=0上的一个动点,O为坐标原点,直线l1:x+y+1 2020-10-31 …
已知点P(pp,如p-o)是平面直角坐标系上的点.(o)若点P在第一象限的角平分线上,求p的值;(p 2020-12-25 …
已知直线y=kx+b经过点A(3,-1)与点B(-6,5).(1)已知点P(-3,t)在该直线上,求 2021-01-11 …