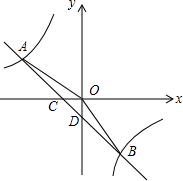
如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于第二、四象限内的A，B两点，与x轴交于点C，与y轴交于点D，点B的坐标是（m，-4），连接AO，AO=5，sin∠AOC=35．（1）求反

Question

如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于第二、四象限内的A，B两点，与x轴交于点C，与y轴交于点D，点B的坐标是（m，-4），连接AO，AO=5，sin∠AOC=(3)/(5)．

（1）求反比例函数的解析式；
（2）连接OB，求△AOB的面积．

Answer 1

（1）过点A作AE⊥x轴于点E，如图所示．

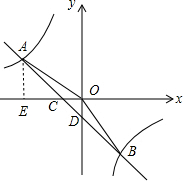
设反比例函数解析式为y=(k)/(x)．
∵AE⊥x轴，
∴∠AEO=90°．
在Rt△AEO中，AO=5，sin∠AOC=(3)/(5)，∠AEO=90°，
∴AE=AO•sin∠AOC=3，OE=√(AO2-AE2)=4，
∴点A的坐标为（-4，3）．
∵点A（-4，3）在反比例函数y=(k)/(x)的图象上，
∴3=(k)/(-4)，解得：k=-12．
∴反比例函数解析式为y=-(12)/(x)．
（2）∵点B（m，-4）在反比例函数y=-(12)/(x)的图象上，
∴-4=-(12)/(m)，解得：m=3，
∴点B的坐标为（3，-4）．
设直线AB的解析式为y=ax+b，
将点A（-4，3）、点B（3，-4）代入y=ax+b中得：

3=-4a+b

-4=3a+b

，解得：

a=-1

b=-1

，
∴一次函数解析式为y=-x-1．
令一次函数y=-x-1中y=0，则0=-x-1，
解得：x=-1，即点C的坐标为（-1，0）．
S_△AOB=(1)/(2)OC•（y_A-y_B）=(1)/(2)×1×[3-（-4）]=(7)/(2)．