早教吧作业答案频道 -->数学-->
如图,抛物线y=12x2+mx+n交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.(1)求这条抛物线的函数关系式;(2)设抛物线与
题目详情
如图,抛物线y=
x2+mx+n交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
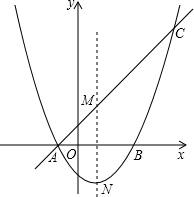
(1)求这条抛物线的函数关系式;
(2)设抛物线与直线的另一交点为C,已知P为线段AC上一点(不含端点),过点P作PQ⊥x轴,交抛物线于点Q,设点P的横坐标为x,用含x的代数式表示线段PQ的长,并求出PQ的最大值;
(3)若点D在抛物线的对称轴上,点E在抛物线上,是否存在以A、B、D、E为顶点的四边形为平行四边形?若存在,求出点E的坐标;若不存在,请说明理由.
| 1 |
| 2 |

(1)求这条抛物线的函数关系式;
(2)设抛物线与直线的另一交点为C,已知P为线段AC上一点(不含端点),过点P作PQ⊥x轴,交抛物线于点Q,设点P的横坐标为x,用含x的代数式表示线段PQ的长,并求出PQ的最大值;
(3)若点D在抛物线的对称轴上,点E在抛物线上,是否存在以A、B、D、E为顶点的四边形为平行四边形?若存在,求出点E的坐标;若不存在,请说明理由.
▼优质解答
答案和解析
(1)∵x=-
=-
=1,
∴m=-1.
∵点M与点N关于x轴对称,
∴点N的坐标为(1,-2).
将m=-1,x=1,y=-2代入得:
-1+n=-2.
解得:n=-
.
∴抛物线的解析式为y=
x2-x-
.
(2)如图1所示:
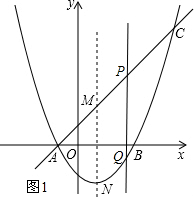
令y=0得:
x2-x-
=0.
解得:x1=-1,x2=3.
则点A的坐标为(-1,0).
设直线AM的解析式为y=kx+b,将点A(-1,0),M(1,2)代入得;
,
解得:k=1,b=1.
∴直线AM的解析式为y=x+1.
∵点P的横坐标为x,PQ⊥x轴,
∴点Q的横坐标为x.
∴点P的纵坐标为x+1,点Q的纵坐标为
x2-x-
.
∴PQ=x+1-(
x2-x-
)=-
x2+2x+
.
∵PQ=-
x2+2x+
=-
(x-2)2+
,
∴当x=2时,PQ有最大值,最大值为
.
(3)如图2所示:
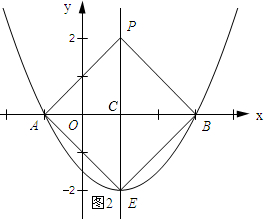
①当AC=BC,PC=CE时,四边形AEBP是平行四边形,此时点E的坐标为(1,-2).
如图3所示:
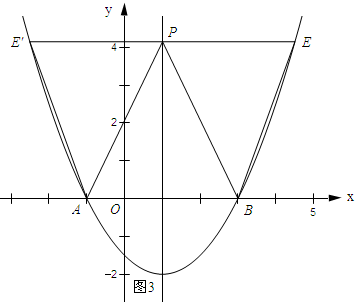
②∵ABPE为平行四边形,
∴PE∥AB,且PE=AB=4.
∴点E的横坐标为5.
将x=5代入y=-
x2-x-
,得y=6.
∴点E的坐标为(5,6).
③∵ABPE′为平行四边形,
∴PE′∥AB,且PE′=AB=4.
∴点E′的横坐标为-3.
将x=-3代入y=-
| b |
| 2a |
| m | ||
|
∴m=-1.
∵点M与点N关于x轴对称,
∴点N的坐标为(1,-2).
将m=-1,x=1,y=-2代入得:
| 1 |
| 2 |
解得:n=-
| 3 |
| 2 |
∴抛物线的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)如图1所示:

令y=0得:
| 1 |
| 2 |
| 3 |
| 2 |
解得:x1=-1,x2=3.
则点A的坐标为(-1,0).
设直线AM的解析式为y=kx+b,将点A(-1,0),M(1,2)代入得;
|
解得:k=1,b=1.
∴直线AM的解析式为y=x+1.
∵点P的横坐标为x,PQ⊥x轴,
∴点Q的横坐标为x.
∴点P的纵坐标为x+1,点Q的纵坐标为
| 1 |
| 2 |
| 3 |
| 2 |
∴PQ=x+1-(
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∵PQ=-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∴当x=2时,PQ有最大值,最大值为
| 9 |
| 2 |
(3)如图2所示:

①当AC=BC,PC=CE时,四边形AEBP是平行四边形,此时点E的坐标为(1,-2).
如图3所示:

②∵ABPE为平行四边形,
∴PE∥AB,且PE=AB=4.
∴点E的横坐标为5.
将x=5代入y=-
| 1 |
| 2 |
| 3 |
| 2 |
∴点E的坐标为(5,6).
③∵ABPE′为平行四边形,
∴PE′∥AB,且PE′=AB=4.
∴点E′的横坐标为-3.
将x=-3代入y=-
作业帮用户
2017-05-28
看了 如图,抛物线y=12x2+m...的网友还看了以下:
二次函数题目抛物线过A(4,0)B(1,0)C(0,-2)三点问一:直线AC上方抛物线找一点D使得 2020-05-13 …
数学(二次函数)1.已知抛物线过A(-2,0),B(1,0),C(0,2)三点在这条抛物线上是否存 2020-05-13 …
(2010•崇明县二模)已知:如图,AC=BC,∠ACB=90°,点B的坐标为(1,0),抛物线过 2020-05-17 …
已知直线过A(3,0),B(0,2)两点,求直线AB方程 2020-05-23 …
直线过A(1,0)且与抛物线y∧2=-2x仅有一个公共点,这样的直线共有几条?直线过A(1,0)且 2020-06-03 …
直线过(a,0),(0,b),(1,3)三点,且a,b为正整数,求此直线方程 2020-06-12 …
在平面坐标系中抛物线过A(-4,0)B(0,-4)C(2,0)三点点M第三象限内抛物线上动点,点M 2020-06-14 …
直线过A(3,4),B(4,0)两点,现直线绕A点顺时针旋转45度,问所得新的直线函数关系式 2020-06-20 …
(2014•义乌市)如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=O 2020-06-29 …
圆的切线割线方程若有一点A(x0,y0),圆(x-a)^2+(y-b)^2=r^2直线过A与圆相切 2020-07-22 …