早教吧作业答案频道 -->数学-->
如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A-B-C运动,设点P运动的时间为t秒.(1)当t为何值时,点P与点A的距离为5cm?(2)当t为何值时,△APD是等
题目详情
如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A-B-C运动,设点P运动的时间为t秒.
(1)当t为何值时,点P与点A的距离为5cm?
(2)当t为何值时,△APD是等腰三角形?
(3)当t为何值时,(2<t<5),以线段AD、CP、AP的长度为三边长的三角形是直角三角形,且AP是斜边?

(1)当t为何值时,点P与点A的距离为5cm?
(2)当t为何值时,△APD是等腰三角形?
(3)当t为何值时,(2<t<5),以线段AD、CP、AP的长度为三边长的三角形是直角三角形,且AP是斜边?
▼优质解答
答案和解析
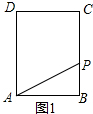 (1)如图1,若点P在BC上,
(1)如图1,若点P在BC上,
∵在Rt△ABP中,AP=5,AB=4
∴BP=2t-4=3,
∴t=
;
如图2,若点P在DC上,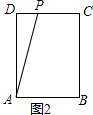
则在Rt△ADP中,AP是斜边,
∵AD=6,
∴AP>6,
∴AP≠5.
综上所述,当t=
秒时,点P与点A的距离为5cm;
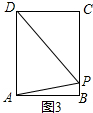
(2)当AD=DP时,如图3,PC=(10-2t)cm,CD=4cm,DP=6cm,
∵CD2+PC2=DP2,即42+(10-2t)2=62,解得t=5±
,即t1=5+
,t2=5-
;
当DP=AP时,如图4,PC=PB=3cm,
∵AB=4cm,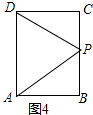
∴AB+BP=4+3=7cm,
∴t=
(秒);
当AD=AP=6时,PB=2t-4,
∵AB2+BP2=AP2,即42+(2t-4)2=62,解得t=2+
或t=2-
(舍去),
综上所述,当t=(5±
)秒或t=
秒时,△APD是等腰三角形;
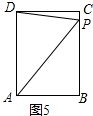
(3)当2<t<5时,点P在BC边上,
∵BP=2t-4,CP=10-2t,
∴AP2=AB2+BP2=42+(2t-4)2
由题意,有AD2+CP2=AP2
∴62+(10-2t)2=42+(2t-4)2
∴t=
<5,
∴t=
.
答:当t=
秒时,以线段AD、CP、AP的长度为三边长的三角形是直角三角形,且AP是斜边.
 (1)如图1,若点P在BC上,
(1)如图1,若点P在BC上,∵在Rt△ABP中,AP=5,AB=4
∴BP=2t-4=3,
∴t=
| 7 |
| 2 |
如图2,若点P在DC上,

则在Rt△ADP中,AP是斜边,
∵AD=6,
∴AP>6,
∴AP≠5.
综上所述,当t=
| 7 |
| 2 |

(2)当AD=DP时,如图3,PC=(10-2t)cm,CD=4cm,DP=6cm,
∵CD2+PC2=DP2,即42+(10-2t)2=62,解得t=5±
| 5 |
| 5 |
| 5 |
当DP=AP时,如图4,PC=PB=3cm,
∵AB=4cm,

∴AB+BP=4+3=7cm,
∴t=
| 7 |
| 2 |
当AD=AP=6时,PB=2t-4,
∵AB2+BP2=AP2,即42+(2t-4)2=62,解得t=2+
| 5 |
| 5 |
综上所述,当t=(5±
| 5 |
| 7 |
| 2 |

(3)当2<t<5时,点P在BC边上,
∵BP=2t-4,CP=10-2t,
∴AP2=AB2+BP2=42+(2t-4)2
由题意,有AD2+CP2=AP2
∴62+(10-2t)2=42+(2t-4)2
∴t=
| 13 |
| 3 |
∴t=
| 13 |
| 3 |
答:当t=
| 13 |
| 3 |
看了 如图,长方形ABCD中,AB...的网友还看了以下:
若M为不等式组{x小于等于0,y大于等于0,y-x小于等于2表示的平面区域,则当a从-2连续变化到 2020-05-13 …
质量为m的小球,在水中受浮力F为常数,当它从静止开始下沉时,受到水的阻力为f=-kv,k为常数,求 2020-05-13 …
这段话怎么解释,我看不懂.还有“△ng”是什么意思.对于有气体参与的可逆反应从反应混合气的平均相对 2020-05-15 …
甲车从M点、乙车从N点同时相向运动,它们的s-t图象分别如图(a)、(b)所示,当甲、乙相遇时.乙 2020-05-16 …
如图,在平面直角坐标系xOy中,已知A(9,0)、B(9,12),点M、N分别是线段OB、AB上的 2020-06-14 …
有一质量为M,半径为R的密度均匀球体,在距离球心O为2R的地方有一质量为m的质点,现从M中挖去一半 2020-07-31 …
如图所示,离质量为M、半径为R、密度均匀的球体表面R远处有一质量为m的质点,此时M对m的万有引力为 2020-07-31 …
(2014•常德二模)如图所示,一不可伸长的轻绳通过光滑的定滑轮,系着质量均为m的物体A和B,A放在 2020-11-12 …
在n个人的班级中,选出m个人参加大扫除,其中k个人擦窗户,其他人拖地板.现有两种方法选择人选:①先从 2021-01-02 …
一袋中有m(m∈N*)个红球,3个黑球和2个白球,现从中任取2个球.(1)当m=4时,求取出的2个球 2021-01-12 …