早教吧作业答案频道 -->数学-->
如图1,在锐角△ABC中,D、E分别是AB、BC的中点,点F在AC上,且满足∠AFE=∠A,DM∥EF交AC于点M.(1)证明:DM=DA;(2)点G在BE上,且∠BDG=∠C,如图2,求证:△DEG∽△ECF;(3)在图2中,取CE
题目详情
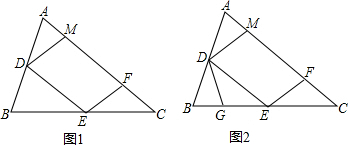
如图1,在锐角△ABC中,D、E分别是AB、BC的中点,点F在AC上,且满足∠AFE=∠A,DM∥EF交AC于点M.
(1)证明:DM=DA;
(2)点G在BE上,且∠BDG=∠C,如图2,求证:△DEG∽△ECF;
(3)在图2中,取CE上一点H,使得∠CFH=∠B,若BG=5,求EH的长.
(1)证明:DM=DA;
(2)点G在BE上,且∠BDG=∠C,如图2,求证:△DEG∽△ECF;
(3)在图2中,取CE上一点H,使得∠CFH=∠B,若BG=5,求EH的长.

▼优质解答
答案和解析
(1)证明:如图1所示,
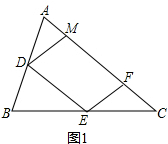 ∵DM∥EF,
∵DM∥EF,
∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)证明:如图2所示,
∵D、E分别是AB、BC的中点,
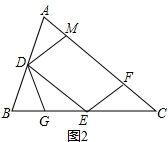 ∴DE∥AC,
∴DE∥AC,
∴∠BDE=∠A,∠DEG=∠C,
∵∠AFE=∠A,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠GDE=∠FEC,
∴△DEG∽△ECF;
(3) 如图3所示,
∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴
=
,
∴BD2=BG•BE,
∵∠AFE=∠A,∠CFH=∠B,
∴∠C=180°-∠A-∠B=180°-∠AFE-∠CFH=∠EFH,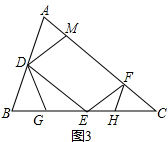
又∵∠FEH=∠CEF,
∴△EFH∽△ECF,
∴
=
,
∴EF2=EH•EC,
∵DE∥AC,DM∥EF,
∴四边形DEFM是平行四边形,
∴EF=DM=DA=BD,
∴BG•BE=EH•EC,
∵BE=EC,
∴EH=BG=5.
 ∵DM∥EF,
∵DM∥EF,∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)证明:如图2所示,
∵D、E分别是AB、BC的中点,
 ∴DE∥AC,
∴DE∥AC,∴∠BDE=∠A,∠DEG=∠C,
∵∠AFE=∠A,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠GDE=∠FEC,
∴△DEG∽△ECF;
(3) 如图3所示,
∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴
| BD |
| BE |
| BG |
| BD |
∴BD2=BG•BE,
∵∠AFE=∠A,∠CFH=∠B,
∴∠C=180°-∠A-∠B=180°-∠AFE-∠CFH=∠EFH,

又∵∠FEH=∠CEF,
∴△EFH∽△ECF,
∴
| EH |
| EF |
| EF |
| EC |
∴EF2=EH•EC,
∵DE∥AC,DM∥EF,
∴四边形DEFM是平行四边形,
∴EF=DM=DA=BD,
∴BG•BE=EH•EC,
∵BE=EC,
∴EH=BG=5.
看了 如图1,在锐角△ABC中,D...的网友还看了以下:
假设U=F(G(X)+Y),其中Y=Y(X)由方程Y方+e的y方=SIN(X+Y)确定,而且F,G 2020-05-14 …
已知奇数f(x)的定义域为(-∞,0)U(0,+∞),且f(x)在(0,+∞)上是减函数,f(1) 2020-05-19 …
已知f(x)=ax^2=bx+c,g(x)=-bx,其中a>b>c且f(1)=0,设方程f(x)= 2020-06-02 …
这是一道“狗什么不通”的shuxue题,真是恼人啊注:2代表的都是二次方.已知f[f(x)]=x2 2020-06-27 …
若f(x)是奇函数,g(x)是偶函数,且f[g(x)]有意义,则f[g(x)]是()A.偶函数B. 2020-08-01 …
定积分比较大小的问题教材上说如果函数f、g在[a,b]可积,并且f≥g在[a,b]上成立,那么∫ab 2020-11-01 …
考验智商极限的问题我说的问题叙述起来都不复杂:f(x),g(x)都在[0,1]上连续,而且f[g(x 2020-11-06 …
求解多元一次不等式的编程47a-b-c-d-e-f-g>047b-a-c-d-e-f-g>023c- 2020-12-14 …
一道数学题,急……设f(x)=ax²+bx+c,(a>b>c),且f(1)=0,g(x)=ax+b. 2020-12-28 …
若二次函数g(x)的图象与一次函数f(x)的图象相切,也与x轴相切,且f[g(x)]=g[f(x)] 2021-01-11 …