已知函数f(x)=alnxx(a∈R)的图象与直线x-2y=0相切，当函数g（x）=f（f（x））-t恰有一个零点时，实数t的取值范围是（）A.{0}B.[0，1]C.[0，1）D.（-∞，0）

Question

已知函数f(x)=

(alnx)/(x)(a∈R)的图象与直线x-2y=0相切，当函数g（x）=f（f（x））-t恰有一个零点时，实数t的取值范围是（　　）

A. {0}

B. [0，1]

C. [0，1）

D. （-∞，0）

Answer 1

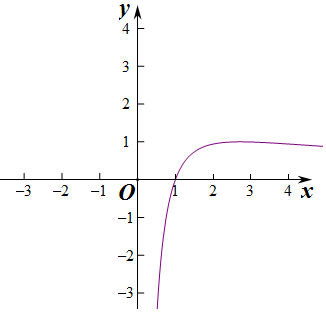由题意，f′（x）=(a(1-lnx))/(x2)，
取切点（m，n），则n=(alnm)/(m)，m=2n，(a(1-lnm))/(m2)=(1)/(2)，
∴a=e．∴f（x）=(elnx)/(x)，
f′（x）=(e(1-lnx))/(x2)，函数f（x）在（0，e）上单调递增，（e，+∞）上单调递减，
f（1）=0，x→+∞，f（x）→0，
由于f（e）=1，f（1）=0，
∴当函数g（x）=f（f（x））-t恰有一个零点时，实数t的取值范围是{0}，
故选A．