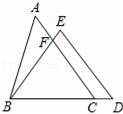
如图，在△ABC和△BDE中，点C在边BD上，边AC交边BE于点F．若AC=BD，AB=ED，BC=BE，则∠ACB等于（）A．∠EDBB．∠BEDC．∠AFBD．2∠ABF

Question

如图，在△ABC和△BDE中，点C在边BD上，边AC交边BE于点F．若AC=BD，AB=ED，BC=BE，则∠ACB等于（　　）

A．∠EDB    B．∠BED    C．∠AFB  D．2∠ABF

Answer 1

C【考点】全等三角形的判定与性质．

【分析】根据全等三角形的判定与性质，可得∠ACB与∠DBE的关系，根据三角形外角的性质，可得答案．

【解答】在△ABC和△DEB中，

，

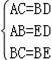
∴△ABC≌△DEB （SSS），

∴∠ACB=∠DBE．

∵∠AFB是△BFC的外角，

∴∠ACB+∠DBE=∠AFB，

∠ACB=∠AFB，

故选：C．

【点评】本题考查了全等三角形的判定与性质，利用了全等三角形的判定与性质，三角形外角的性质．