早教吧作业答案频道 -->数学-->
如图:△ABC是O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作O的切线交AB的延长线于点D.(1)求证:CD=CB;(2)如果O的半径为2,求AC的长.
题目详情
如图:△ABC是 O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作 O的切线交AB的延长线于点D.
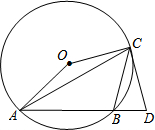
(1)求证:CD=CB;
(2)如果 O的半径为
,求AC的长.

(1)求证:CD=CB;
(2)如果 O的半径为
| 2 |
▼优质解答
答案和解析
(1)证明:连接OB,则∠AOB=2∠ACB=2×45°=90°,
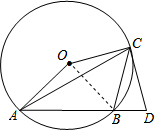 ∵OA=OB,
∵OA=OB,
∴∠OAB=OBA=45°,
∵∠AOC=150°,OA=OC,
∴∠OCA=∠OAC=15°,
∴∠OCB=∠OCA+∠ACB=60°,
∴△OBC是等边三角形,
∴∠BOC=∠OBC=60°,
∴∠CBD=180°-∠OBA-∠OBC=75°,
∵CD是 O的切线,
∴OC⊥CD,
∴∠D=360°-∠OBD-∠BOC-∠OCD=360°-(60°+75°)-60°-90°=75°,
∴∠CBD=∠D,
∴CB=CD;
(2)在Rt△AOB中,AB=
OA=
×
=2,
∵CD是 O的切线,
∴∠DCB=∠CAD,
∵∠D是公共角,
∴△DBC∽△DCA,
∴
=
,
∴CD2=AD•BD=BD•(BD+AB),
∵CD=BC=OC=
,
∴2=BD•(2+BD),
解得:BD=
-1,
∴AC=AD=AB+BD=
+1.
 ∵OA=OB,
∵OA=OB,∴∠OAB=OBA=45°,
∵∠AOC=150°,OA=OC,
∴∠OCA=∠OAC=15°,
∴∠OCB=∠OCA+∠ACB=60°,
∴△OBC是等边三角形,
∴∠BOC=∠OBC=60°,
∴∠CBD=180°-∠OBA-∠OBC=75°,
∵CD是 O的切线,
∴OC⊥CD,
∴∠D=360°-∠OBD-∠BOC-∠OCD=360°-(60°+75°)-60°-90°=75°,
∴∠CBD=∠D,
∴CB=CD;
(2)在Rt△AOB中,AB=
| 2 |
| 2 |
| 2 |
∵CD是 O的切线,
∴∠DCB=∠CAD,
∵∠D是公共角,
∴△DBC∽△DCA,
∴
| CD |
| AD |
| BD |
| CD |
∴CD2=AD•BD=BD•(BD+AB),
∵CD=BC=OC=
| 2 |
∴2=BD•(2+BD),
解得:BD=
| 3 |
∴AC=AD=AB+BD=
| 3 |
看了 如图:△ABC是O的内接三角...的网友还看了以下:
刚刚学...(我代我同学问来着..)1.已知直角三角形的两条直角边为a和b.斜边为c.(1)如果a= 2020-03-30 …
分解因式X的二次方+AX+B,甲看错了A的值,结果是(X+6)乙看错了B结果是(X-2)(X=1) 2020-04-27 …
excel中根据某列的值选择函数中的标准值比如如果A列中的值≥20的,则要求B、C、D、E列值分别 2020-05-13 …
一道匀变速直线运动的追及问题A车和B车相距10m.A车初速度为10m/s,加速度为1m/s2;B车 2020-05-23 …
给定一非对称矩阵,求一非零对称矩阵与之相乘,使乘积仍为对称矩阵对任意矩阵A,求非零对称矩阵B表达式 2020-06-10 …
设P(A)=a,P(B)=b.如果AB不相容,求P(AUB)=如果AB相互独立.求P(AUB)=如 2020-06-12 …
解决一道应用题.小彬和小红相约一起去乐乐超市买果汁,你能根据他们的对话内容,求出A.B两种果汁的单 2020-07-06 …
假设消费者的嗜好转向苹果消费.以下哪一种说法是对苹果市场上这个事件影响的正确描述().A.苹果的需 2020-07-13 …
1.X:16=5:122.4:0.6=X:93.15分之X=6分之54.X+2分之6=3分之25. 2020-08-02 …
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x^2-2x(1)求当x<0时,f(x)的解 2020-12-03 …