早教吧作业答案频道 -->数学-->
如图,O的半径为1,A,P,B,C是O上的四个点,∠APC=∠CPB=60°.(1)判断△ABC的形状:;(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;(3)当点P位于
题目详情
如图, O的半径为1,A,P,B,C是 O上的四个点,∠APC=∠CPB=60°.
(1)判断△ABC的形状:___;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于
的什么位置时,四边形APBC的面积最大?求出最大面积.
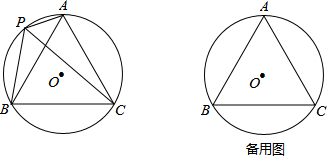
(1)判断△ABC的形状:___;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于
 |
| AB |

▼优质解答
答案和解析
证明:(1)△ABC是等边三角形.
证明如下:在 O中
∵∠BAC与∠CPB是
所对的圆周角,∠ABC与∠APC是
所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)在PC上截取PD=AP,如图1,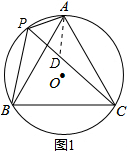
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP;
(3)当点P为
的中点时,四边形APBC的面积最大.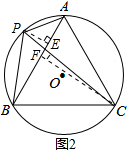
理由如下,如图2,过点P作PE⊥AB,垂足为E.
过点C作CF⊥AB,垂足为F.
∵S△APB=
AB•PE,S△ABC=
AB•CF,
∴S四边形APBC=
AB•(PE+CF),
当点P为
的中点时,PE+CF=PC,PC为 O的直径,
∴此时四边形APBC的面积最大.
又∵ O的半径为1,
∴其内接正三角形的边长AB=
,
∴S四边形APBC=
×2×
=
.
证明如下:在 O中
∵∠BAC与∠CPB是
 |
| BC |
 |
| AC |
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)在PC上截取PD=AP,如图1,

又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
|
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP;
(3)当点P为
 |
| AB |

理由如下,如图2,过点P作PE⊥AB,垂足为E.
过点C作CF⊥AB,垂足为F.
∵S△APB=
| 1 |
| 2 |
| 1 |
| 2 |
∴S四边形APBC=
| 1 |
| 2 |
当点P为
 |
| AB |
∴此时四边形APBC的面积最大.
又∵ O的半径为1,
∴其内接正三角形的边长AB=
| 3 |
∴S四边形APBC=
| 1 |
| 2 |
| 3 |
| 3 |
看了 如图,O的半径为1,A,P,...的网友还看了以下:
已知A(-2,1+3),B(2,1−3),P(-1,1),若直线l过点P且与线段AB有公共点,则直 2020-04-11 …
设全集U={1,2,3,4,5,6},集合A={1,2,3},B={2,4,5},则CU(A∩B) 2020-07-15 …
冬季蚌埠市某三天的最低气温分别是-6℃,1℃,-4℃,把它们从高到低排列正确的是()A.1℃,-4℃ 2020-11-12 …
冬季蚌埠市某三天的最低气温分别是-6℃,1℃,-4℃,把它们从高到低排列正确的是()A.1℃,-4℃ 2020-11-12 …
位于拉萨(29°36′N,91°06′E)的中学生收看授课直播,当地区时是()A.6月20日8时B. 2020-11-28 …
福建6月份的太阳辐射强度比l2月份大,主要原因是()A.6月份晴天比12月份多B.6月份正午太阳高度 2020-12-01 …
如果零上3℃记作+3℃,那么零下6℃记作()A.6℃B.-6℃C.6D.-6 2020-12-27 …
如果零上6℃计作+6℃,那么零下6℃记作()A.-6℃B.6℃C.6D.-6 2020-12-27 …
第十九届世界杯开幕式于南非当地时间(东二区区时)2010年6月11日14时举行,杭州球迷开始观看开幕 2021-01-09 …
根据2010年第六次全国人口普查主要数据公报,嵊州市常住人口为679762人.这个数据可以用科学记数 2021-01-12 …