已知：如图，在等腰三角形ABC中，120°<∠BAC<180°，AB=AC，AD⊥BC于点D．以AC为边作等边三角形ACE，△ACE与△ABC在直线AC的异侧，直线BE交直线AD于点F，连接FC交AE于点M．（1）求证：∠FEA=

Question

已知：如图，在等腰三角形ABC中，120°<∠BAC<180°，AB=AC，AD⊥BC于点D．以AC为边作等边三角形ACE，△ACE与△ABC在直线AC的异侧，直线BE交直线AD于点F，连接FC交AE于点M． 

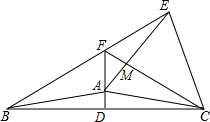
（1）求证：∠FEA=∠FCA；
（2）猜想线段FE，FA，FD之间的数量关系，并证明你的结论．

Answer 1

（1）证明：如图1，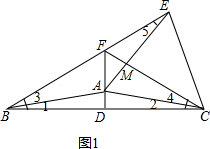

∵AB=AC，
∴∠1=∠2，
∵AD⊥BC，
∴直线AD垂直平分BC，
∴FB=FC，
∴∠FBC=∠FCB，
∴∠FBC-∠1=∠FCB-∠2，
即∠3=∠4，
∵等边三角形ACE中，AC=AE，
∴AB=AE，
∴∠3=∠5，
∴∠4=∠5，
即∠FEA=∠FCA；

（2）FE+FA=2FD，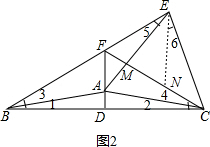
证明：在FC上截取FN，使FN=FE，连接EN，如图2，
∵∠FME=∠AMC，∠5=∠4，
∴180°-∠5-∠FME=180°-∠4-∠AMC，
∴∠EFM=∠CAM，
∵等边三角形ACE中，∠CAE=60°，
∴∠EFM=60°，
∵FN=FE，
∴△EFN是等边三角形，
∴∠FEN=60°，EN=EF，
∵△ACE为等边三角形，
∴∠AEC=60°，EA=EC，
∴∠FEN=∠AEC，
∴∠FEN-∠MEN=∠AEC-∠MEN，
即∠5=∠6，
在△EFA和∠ENC中，

EF=EN

∠5=∠6

EA=EC

∴△EFA≌△ENC，
∴FA=NC，
∴FE+FA=FN+NC=FC，
∵∠EFC=∠FBC+∠FCB=60°，∠FBC=∠FCB，
∴∠FCB=(1)/(2)×60°=30°，
∵AD⊥BC，
∴∠FDC=90°，
∴FC=2FD，
∴FE+FA=2FD．