早教吧作业答案频道 -->数学-->
已知点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点(Fermatpoint).已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的
题目详情
已知点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点(Fermat point).已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为
的等腰直角三角形DEF的费马点,则PD+PE+PF=___.
| | 2 |
▼优质解答
答案和解析
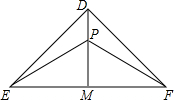 如图:等腰Rt△DEF中,DE=DF=
如图:等腰Rt△DEF中,DE=DF=
,
过点D作DM⊥EF于点M,过E、F分别作∠MEP=∠MFP=30°,
则EM=DM=1,
故cos30°=
,
解得:PE=PF=
=
,则PM=
,
故DP=1-
,
则PD+PE+PF=2×
+1-
=
+1.
故答案为:
+1.
 如图:等腰Rt△DEF中,DE=DF=
如图:等腰Rt△DEF中,DE=DF=| 2 |
过点D作DM⊥EF于点M,过E、F分别作∠MEP=∠MFP=30°,
则EM=DM=1,
故cos30°=
| EM |
| EP |
解得:PE=PF=
| 2 | ||
|
2
| ||
| 3 |
| ||
| 3 |
故DP=1-
| ||
| 3 |
则PD+PE+PF=2×
2
| ||
| 3 |
| ||
| 3 |
| 3 |
故答案为:
| 3 |
看了 已知点P是△ABC内一点,且...的网友还看了以下:
1.一个长72cm的铁丝制作成一个长9cm,宽3cm的长方形框架,这个框架高多少厘米?2.一个长1 2020-05-22 …
1若a,b,x,y属于正数,证明:x分之a平方+y分之b平方大于等于(x+y)分之(a+b)的平方 2020-06-02 …
2.证明:(1)a,b为不等的正整数,1/a、1/b的算术平均值为1/6==>a、b的算术;2.证 2020-06-13 …
公式a*b/(a-1)还能解吗公式a*b*(a-1)=a*b*a-a*b这个成立,公式a*b/(a 2020-07-17 …
设a,b,c都是正数且a+b+c=1,求证:(1+a)(1+b)(1+c)≥8(1-a)(1-b) 2020-07-25 …
两个应用题解答1.一个高为3分米的圆锥体,如果沿高平均切成两个半圆锥,这时的切面正好是一个等腰直角 2020-07-31 …
用一个字形容历史朝代简介1.十个历史朝代,分别为夏、商、秦、汉、周、唐、宋、元、明、清.2.分别用 2020-08-03 …
已知a>0,b>0且a+b=1,则(1/a^2-1)(1/b^2-1)的最小值是多少?(1/a²-1 2020-11-01 …
阅读下列例题例ab=1,试求代数式a/(a+1)+b/(b+1)的值因为ab=1,所以a/a+1=a 2020-11-28 …
看看是什么三角形以知三角形ABC的三边分别为abc,且满足1/a-1/b+1/c=1/a-b+c试判 2020-12-25 …