早教吧作业答案频道 -->数学-->
已知抛物线C:x2=2py(p>0)过点(2,1),直线l过点P(0,-1)与抛物线C交于A、B两点,点A关于y轴的对称点为A′,连接A′B(1)求抛物线C的标准方程;(2)问直线A'B是否过定点?若是
题目详情
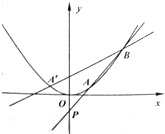
已知抛物线C:x2=2py(p>0)过点(2,1),直线l过点P(0,-1)与抛物线C交于A、B两点,点A关于y轴的对称点为A′,连接A′B
(1)求抛物线C的标准方程;
(2)问直线A'B是否过定点?若是,求长定点坐标;若不是,请说明理由.

(1)求抛物线C的标准方程;
(2)问直线A'B是否过定点?若是,求长定点坐标;若不是,请说明理由.
▼优质解答
答案和解析
(1)将点(2,1)代入抛物线x2=2py的方程得,p=2,
所以,抛物线C的标准方程为x2=4y. …(4分)
(2)设直线l的方程为y=kx-1,又设A(x1,y1),B(x2,y2),则A'(-x1,y1),
由
得x2-4kx+4=0,则△=16k2-16>0,x1•x2=4,x1+x2=4k,
所以kA′B=
=
=
,
于是直线A'B的方程为y-
=
(x-x2),…(8分)
所以,y=
(x-x2)+
=
x+1,当x=0时,y=1,
所以直线A'B过定点(0,1). …(10分)
所以,抛物线C的标准方程为x2=4y. …(4分)
(2)设直线l的方程为y=kx-1,又设A(x1,y1),B(x2,y2),则A'(-x1,y1),
由
|
所以kA′B=
| y2-y1 |
| x2-(-x1) |
| ||||
| x1+x2 |
| x2-x1 |
| 4 |
于是直线A'B的方程为y-
| x22 |
| 4 |
| x2-x1 |
| 4 |
所以,y=
| x2-x1 |
| 4 |
| x22 |
| 4 |
| x2-x1 |
| 4 |
所以直线A'B过定点(0,1). …(10分)
看了 已知抛物线C:x2=2py(...的网友还看了以下:
抛物线方程为x^2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为 2020-05-13 …
已知X1和X2是一元二次方程4倍K乘以X的平方减4倍KX加K加1等于0的两个实数根.1.是否存在实 2020-05-16 …
在平面直角座标系中直线I与抛物线X的平方=2Y相交于A,B两点求如果I过点(0.3)求证向量OA* 2020-06-14 …
1、已知一元二次方程x²-2x-1=0的两个根分别为X1X2求x1+x2+2x1、x2的值X1和X 2020-07-18 …
已知M1,M2是抛体运动轨迹上的两点,K为轨迹长度,求抛物线方程已知M1(x1,y1,z1),M2 2020-07-20 …
现代人为什么会越来越有不安全感?物质与心理是1一体的两面,过度的追求物质方向,会让人类的精神崩溃! 2020-07-25 …
解析几何已知抛物线y^2=2px(p0)与圆x^2+y^2=4的公共弦长为根号(12).求p;将抛 2020-08-01 …
求物理方面的人才,如果施加力可以注射喷头的水喷射10米高(远),那是不是可以估计喷头的水压为0.1M 2020-11-10 …
第一个,已知x1x2是方程3x方-2x-7=0的两个根,不解方程,利用根与系数的关系,求(x1-x2 2020-11-24 …
求物探方面的非金属声波探测仪(做钻孔的那个设备)的相关知识,包括设备原理,使用方法及注意事项等,有图 2020-12-03 …