早教吧作业答案频道 -->数学-->
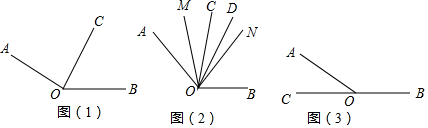
已知∠AOB=150°,OD为∠AOB内部的一条射线(1)如图(1),若∠BOC=60°,OD为∠AOB内部的一条射线,∠COD=13∠BOC,OE平分∠AOB,求∠DOE的度数.(2)如图(2),若OC、OD
题目详情
已知∠AOB=150°,OD为∠AOB内部的一条射线
(1)如图(1),若∠BOC=60°,OD为∠AOB内部的一条射线,∠COD=
∠BOC,OE平分∠AOB,求∠DOE的度数.
(2)如图(2),若OC、OD是∠AOB内部的两条射线,OM、ON分别平分∠AOD,∠BOC,且∠MOC≠∠NOD,求(∠AOC-∠BOD)/(∠MOC-∠NOD)的值.
(3)如图(3),C1为射线OB的反向延长线上一点,将射线OB绕点O顺时针以6°/s的速度旋转,旋转后OB对应射线为OB1,旋转时间为t秒(0<t≤35),OE平分∠AOB1,OF为∠C1OB1的三等分线,∠C1OF=
∠C1OB1,若|∠C1OF-∠AOE|=30°,直接写出t的值为___.
(1)如图(1),若∠BOC=60°,OD为∠AOB内部的一条射线,∠COD=
| 1 |
| 3 |
(2)如图(2),若OC、OD是∠AOB内部的两条射线,OM、ON分别平分∠AOD,∠BOC,且∠MOC≠∠NOD,求(∠AOC-∠BOD)/(∠MOC-∠NOD)的值.
(3)如图(3),C1为射线OB的反向延长线上一点,将射线OB绕点O顺时针以6°/s的速度旋转,旋转后OB对应射线为OB1,旋转时间为t秒(0<t≤35),OE平分∠AOB1,OF为∠C1OB1的三等分线,∠C1OF=
| 1 |
| 3 |

▼优质解答
答案和解析
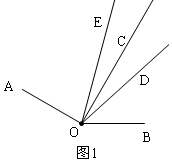 解(1)分两种情况:
解(1)分两种情况:
①当射线OD在∠BOC的内部时,如图1所示,
∵OE平分∠AOB,
∴∠BOE=
∠AOB,
又∠AOB=150°,
∴∠BOE=75°,
又∵∠COD=
∠BOC,且∠BOC=60°,
∴∠BOD=
∠BOC=
×60°=40°,
∴∠DOE=∠BOE-∠BOD=75°-40°=35°;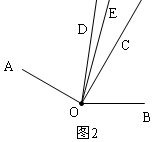
②当射线OD在∠AOC的内部时,
如图2所示,同理得:∠BOE=75°,
∵∠COD=
∠BOC=
×60°=20°,
∴∠DOE=∠COD+∠BOC-∠BOE,
=20°+60°-75°,
=5°,
综上所述,∠DOE=35°或5°;
(2)∵OM、ON分别平分∠AOD,∠BOC,
∴∠MOD=
∠AOD,∠CON=
∠BOC,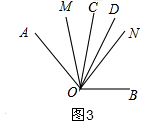
又∠MOC=∠MOD-∠COD,∠NOD=∠CON-∠COD,
∴∠MOC-∠NOD=(∠MOD-∠COD)-(∠CON-∠COD),
=
∠AOD-∠COD-(
∠BOC-∠COD),
=
(∠AOD-∠BOC),
而∠AOD=∠AOC+∠COD,∠BOC=∠BOD+∠COD,
∴∠MOC-∠NOD=
(∠AOC+∠COD-∠BOD-COD),
=
(∠AOC-∠BOD),
∴(∠AOC-∠BOD)/(∠MOC-∠NOD)=
=2;
(3)①当∠BOB1<90°时,
∵∠BOB1=6t,
∴∠AOB1=150°+6t,
∵OE平分∠AOB1,
∴∠AOE=
∠AOB1=
(150°+6t)=75°+3t,
∵∠C1OB1=360°-∠C1OB1=180°-6t,
∵∠C1OF=
∠C1OB1,
∴∠C1OF=60°-2t,
∵|∠C1OF-∠AOE|=30°,
∴75°+3t-60°+2t=30°或60°-2t-75°-3t=30°,
∴t=9,
②当∠BOB1>90°时,
同理t=15,
故答案为:9秒或15秒.
 解(1)分两种情况:
解(1)分两种情况:①当射线OD在∠BOC的内部时,如图1所示,
∵OE平分∠AOB,
∴∠BOE=
| 1 |
| 2 |
又∠AOB=150°,
∴∠BOE=75°,
又∵∠COD=
| 1 |
| 3 |
∴∠BOD=
| 2 |
| 3 |
| 2 |
| 3 |
∴∠DOE=∠BOE-∠BOD=75°-40°=35°;

②当射线OD在∠AOC的内部时,
如图2所示,同理得:∠BOE=75°,
∵∠COD=
| 1 |
| 3 |
| 1 |
| 3 |
∴∠DOE=∠COD+∠BOC-∠BOE,
=20°+60°-75°,
=5°,
综上所述,∠DOE=35°或5°;
(2)∵OM、ON分别平分∠AOD,∠BOC,
∴∠MOD=
| 1 |
| 2 |
| 1 |
| 2 |

又∠MOC=∠MOD-∠COD,∠NOD=∠CON-∠COD,
∴∠MOC-∠NOD=(∠MOD-∠COD)-(∠CON-∠COD),
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
而∠AOD=∠AOC+∠COD,∠BOC=∠BOD+∠COD,
∴∠MOC-∠NOD=
| 1 |
| 2 |
=
| 1 |
| 2 |
∴(∠AOC-∠BOD)/(∠MOC-∠NOD)=
| ∠AOC-∠BOD | ||
|
(3)①当∠BOB1<90°时,
∵∠BOB1=6t,
∴∠AOB1=150°+6t,
∵OE平分∠AOB1,
∴∠AOE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠C1OB1=360°-∠C1OB1=180°-6t,
∵∠C1OF=
| 1 |
| 3 |
∴∠C1OF=60°-2t,
∵|∠C1OF-∠AOE|=30°,
∴75°+3t-60°+2t=30°或60°-2t-75°-3t=30°,
∴t=9,
②当∠BOB1>90°时,
同理t=15,
故答案为:9秒或15秒.
看了 已知∠AOB=150°,OD...的网友还看了以下:
AB是圆O直径,C是圆O上一点,CD⊥AB于D,E为线段CD上一点,直线AE交圆O于E.求证AC² 2020-04-25 …
如图,AB是圆O的直径,CD切圆O于点C,AD交于圆O点E,当AC满足什么条件时,AD垂直于CD, 2020-05-15 …
如图,AB是⊙O的直径,DF切⊙O于点D,BF⊥DF于F,过点A作AC∥BF交BD的延长线于点C. 2020-06-15 …
(2014•营口模拟)如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂 2020-07-22 …
如图,在半径为1的⊙O上任取一点A,连续以1为半径在⊙O上截取AB=BC=CD,分别以A、D为圆心 2020-07-22 …
以圆O外一点P,引圆的两条切线PA,PB,A,B为切点.割线PCD交圆O于C,D.又由B作CD的平 2020-07-31 …
(2010•汉阳区一模)如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平 2020-08-01 …
英语翻译1、OldMacdonaldhadafarm.E-I-E-I-O.Andonthatfarm 2020-11-01 …
排列成正确的句子:me,I,go,excuse,haveto.排列成正确的单词:1.c,d,e,s, 2020-11-01 …
将下列字母重新排列组将下列字母重新排列组成单词,完成句子.1.Daveishis(u,n,c,o,i 2020-12-17 …