早教吧作业答案频道 -->数学-->
如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.(1)请你判断OM和ON的数量关系,并说明理由;(2)过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求
题目详情
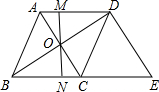
如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
(1)请你判断OM和ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求△BDE的周长.

(1)请你判断OM和ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求△BDE的周长.
▼优质解答
答案和解析
(1)∵四边形ABCD是菱形,
∴AD∥BC,AO=OC,
∴
=
=1,
∴OM=ON.
(2)∵四边形ABCD是菱形,
∴AC⊥BD,AD=BC=AB=6,
∴BO=
=
=2
,
∴BD=2BO=2×2
=4
,
∵DE∥AC,AD∥CE,
∴四边形ACED是平行四边形,
∴DE=AC=8,
∴△BDE的周长是:
BD+DE+BE
=BD+AC+(BC+CE)
=4
+8+(6+6)
=20+4
即△BDE的周长是20+4
.
∴AD∥BC,AO=OC,
∴
| OM |
| ON |
| AO |
| OC |
∴OM=ON.
(2)∵四边形ABCD是菱形,
∴AC⊥BD,AD=BC=AB=6,
∴BO=
| AB2-AO2 |
| 62-(8÷2)2 |
| 5 |
∴BD=2BO=2×2
| 5 |
| 5 |
∵DE∥AC,AD∥CE,
∴四边形ACED是平行四边形,
∴DE=AC=8,
∴△BDE的周长是:
BD+DE+BE
=BD+AC+(BC+CE)
=4
| 5 |
=20+4
| 5 |
即△BDE的周长是20+4
| 5 |
看了 如图,在菱形ABCD中,对角...的网友还看了以下:
如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O交AD于E,交BC于F如图,平行四边形 2020-05-15 …
∵EM是⊙O的切线,怎么推出EB•EC=EM2①?,看题后回答.(2005•温州)如图,已知四边形 2020-05-21 …
三角形ABC为园O的内接三角形,AD为三角形BAC的角平分线,交园O与D,交BC与E,MN//BC 2020-07-22 …
1ab等于ac,角a等于36度,ab得中垂线mn交ac于点d,交ab于点m,求证bd是角abc的平 2020-07-30 …
(1)如图1,在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O 2020-07-31 …
如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点 2020-07-31 …
等边三角形ABC,AB=a,O为三角形的中心,过O点的直线交AB于M,交AC于N,求1.等边三角形 2020-08-03 …
概率论问题,1.ĀUŌ=(AnO)的逆事件?口述:A的逆事件并O的逆事件,等于A交O的逆事件?这个公 2020-11-03 …
阅读下面材料:在数学课上,老师提出如下问题:尺规作如图1:作∠A'O'B'=∠AOB.已知:∠AOB 2020-11-06 …
如图,直线y=-3x+2与x轴交于点C,与y轴交于点B,点A为y轴正半轴上的一点,⊙A经过点B,O, 2021-01-12 …