早教吧作业答案频道 -->数学-->
已知:在△ABC中,AB=AC,AD⊥BC,垂足为D,BE⊥AC,垂足为E,M为AB的中点,联结DE、DM.(1)当∠C=70°时(如图),求∠EDM的度数;(2)当△ABC是钝角三角形时,请画出相应的图形;设∠C=α
题目详情
已知:在△ABC中,AB=AC,AD⊥BC,垂足为D,BE⊥AC,垂足为E,M为AB的中点,联结DE、DM.
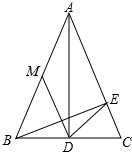
(1)当∠C=70°时(如图),求∠EDM的度数;
(2)当△ABC是钝角三角形时,请画出相应的图形;设∠C=α,用α表示∠EDM(可直接写出).

(1)当∠C=70°时(如图),求∠EDM的度数;
(2)当△ABC是钝角三角形时,请画出相应的图形;设∠C=α,用α表示∠EDM(可直接写出).
▼优质解答
答案和解析
(1)∵AB=AC,AD⊥BC,垂足为D,
∴D为BC中点,∠ABC=∠C=70°,
∵BE⊥AC,∴DE=
BC=DC,
∴∠DEC=∠C=70°,
∴∠EDC=180°-2×70°=40°,
∵AD⊥BC,M为AC的中点,
∴DM=
AB=BM,
∴∠MDB=∠ABC=70°,
∴∠EDM=180°-∠EDC-∠BDM=70°;
(2)如图,∵AB=AC,AD⊥BC,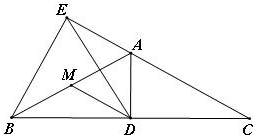
∴D是BC的中点,
又∵BE⊥AC,
∴DE=
BC=DC,
∴∠DEC=∠C=α,
∴∠EDC=180°-∠DEC-∠C=180°-2α,
∵AB=AC,
∴∠ABC=∠C=α,
又∵M是AB的中点,AD⊥BC,
∴DM=
AB=BM,
∴∠MBD=∠MDB=α,
∴∠EDM=180°-∠MDB-∠EDC=α.
∴D为BC中点,∠ABC=∠C=70°,
∵BE⊥AC,∴DE=
| 1 |
| 2 |
∴∠DEC=∠C=70°,
∴∠EDC=180°-2×70°=40°,
∵AD⊥BC,M为AC的中点,
∴DM=
| 1 |
| 2 |
∴∠MDB=∠ABC=70°,
∴∠EDM=180°-∠EDC-∠BDM=70°;
(2)如图,∵AB=AC,AD⊥BC,

∴D是BC的中点,
又∵BE⊥AC,
∴DE=
| 1 |
| 2 |
∴∠DEC=∠C=α,
∴∠EDC=180°-∠DEC-∠C=180°-2α,
∵AB=AC,
∴∠ABC=∠C=α,
又∵M是AB的中点,AD⊥BC,
∴DM=
| 1 |
| 2 |
∴∠MBD=∠MDB=α,
∴∠EDM=180°-∠MDB-∠EDC=α.
看了 已知:在△ABC中,AB=A...的网友还看了以下:
以下各正方形的边长是无理数的是a面积为25的正方形b面积为16的正方形c面积为8的正方形d以下各正 2020-04-27 …
四边形的四条边分别为a,b,c,d,其中a,c为对边,且满足a平方+b平方+c平方=2ab+2cd 2020-05-15 …
已知A,B,C为三角形的三个内角,它们的对边长分别为a,b,c,已知直线xsinA+ysinB+s 2020-05-19 …
已知A,B,C为三角形的三个内角,它们的对边长分别为a,b,c,已知直线xsinA+ysinB+s 2020-05-19 …
已知A,B,C为三角形的三个内角,它们的对边长分别为a,b,c,已知直线xsinA+ysinB+s 2020-05-19 …
1.要画一个三角形,需要知道三个元素,其中至少一个元素是2.三角形的三边长a,b,c,满足b分之a 2020-06-08 …
若a,b,c为△ABC的三边,且(x+a)(x+b)+(x+b)(x+c)+(x+c)(x+a)为 2020-06-12 …
已知a,b,c是△ABC的三边长,如果(c-5)2+|b-12|+a2−26a+169=0,则△A 2020-07-18 …
已知a,b,c是三角形ABC的三边长,(a-5)^2+|b-12|+c^2-26c+169=0,则 2020-07-18 …
在三角形ABC中,AB=根号(a^2+b^2),AC=根号(a^2+c^2),BC=根号(b^2+ 2020-08-03 …