早教吧作业答案频道 -->数学-->
如图,已知△ABC是等边三角形,以AB为直径作O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.(1)求证:DE是O的切线;(2)若△ABC的边长为4,求EF的长度.
题目详情
如图,已知△ABC是等边三角形,以AB为直径作 O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
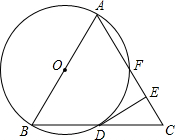
(1)求证:DE是 O的切线;
(2)若△ABC的边长为4,求EF的长度.

(1)求证:DE是 O的切线;
(2)若△ABC的边长为4,求EF的长度.
▼优质解答
答案和解析
(1)证明:如图1,连接OD,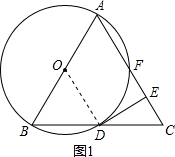
∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵OB=OD,
∴∠ODB=∠B=60°.
∵DE⊥AC,
∴∠DEC=90°.
∴∠EDC=30°.
∴∠ODE=90°.
∴DE⊥OD于点D.
∵点D在 O上,
∴DE是 O的切线;
(2) 如图2,连接AD,BF,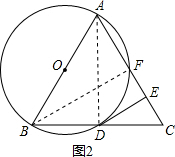
∵AB为 O直径,
∴∠AFB=∠ADB=90°.
∴AF⊥BF,AD⊥BD.
∵△ABC是等边三角形,
∴DC=
BC=2,FC=
AC=2.
∵∠EDC=30°,
∴EC=
DC=1.
∴FE=FC-EC=1.

∵△ABC是等边三角形,
∴∠B=∠C=60°.
∵OB=OD,
∴∠ODB=∠B=60°.
∵DE⊥AC,
∴∠DEC=90°.
∴∠EDC=30°.
∴∠ODE=90°.
∴DE⊥OD于点D.
∵点D在 O上,
∴DE是 O的切线;
(2) 如图2,连接AD,BF,

∵AB为 O直径,
∴∠AFB=∠ADB=90°.
∴AF⊥BF,AD⊥BD.
∵△ABC是等边三角形,
∴DC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠EDC=30°,
∴EC=
| 1 |
| 2 |
∴FE=FC-EC=1.
看了 如图,已知△ABC是等边三角...的网友还看了以下:
(1)光在中沿直线传播,射击瞄准时要做到“三点一线”,这是利用光的的原理,阳光透过树叶间的缝隙射到地 2020-03-30 …
如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分 2020-04-25 …
已知三角形ABC中,分别以AB.AC为边向三角形ABC的形外作正方形ABDE和正方形ACFG,連接 2020-04-27 …
刚从冰箱中取出的冰冻西红柿在冒“白气”,几分钟后西红柿又变成了一个“雪球”,从物态变化的角度分析, 2020-05-13 …
定理:三角形的外心O、重心G、垂心H依次在同一条直线(欧拉线)上,且OG=13OH,其中外心O是三 2020-05-16 …
(1/3)1、三角形OAB固定不动.保持三角形OCD的形状和大小不变,将三角形OCD绕着点O旋转 2020-05-16 …
一道初三函数与几何题如图,直角坐标系内的梯形AOBC,AC∥OB,S△AOC:S△BOC=1:2, 2020-05-17 …
美式发音的问题,o和n连在一起怎么发?Phone,only的音标分别是fon,onli,但是听起来 2020-05-21 …
霜的形成实验,小学六年级科学,希望解答!希望能有具体的实验过程,实验表格,谢谢O(∩∩)O~ 2020-05-21 …
半圆O的圆心O在Rt△ABC的斜边AB上,且圆O分别切AC,BC于D,E两点,BC=a,AC=b, 2020-06-15 …