早教吧作业答案频道 -->数学-->
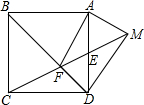
如图,边长为4正方形ABCD中,E为边AD的中点,连接线段EC交BD于点F,点M是线段CE延长线上的一点,且∠MAF为直角,则DM的长为.
题目详情
如图,边长为4正方形ABCD中,E为边AD的中点,连接线段EC交BD于点F,点M是线段CE延长线上的一点,且∠MAF为直角,则DM的长为___.

▼优质解答
答案和解析
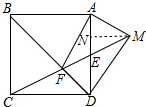 作MN⊥AD垂足为N.
作MN⊥AD垂足为N.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABF=∠CBF,BC∥AD,∠BAD=∠CDA=90°,
∵BF=BF,
∴△BFA≌△BFC,
∴∠BAF=∠BCF=∠CED=∠AEM,
∵∠MAF=∠BAD=90°,
∴∠BAF=∠MAE,
∴∠MAE=∠AEM,
∴MA=ME
∵AE=ED=
AD=2,
∴AN=NE=
AE=1,
∵∠MNE=∠CDE=90°,
∴MN∥CD,
∴
=
=
,
∵CD=4,
∴MN=2,
在RT△MND中,∵MN=2,DN=3,
∴DM=
=
=
,
故答案为
.
 作MN⊥AD垂足为N.
作MN⊥AD垂足为N.∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABF=∠CBF,BC∥AD,∠BAD=∠CDA=90°,
∵BF=BF,
∴△BFA≌△BFC,
∴∠BAF=∠BCF=∠CED=∠AEM,
∵∠MAF=∠BAD=90°,
∴∠BAF=∠MAE,
∴∠MAE=∠AEM,
∴MA=ME
∵AE=ED=
| 1 |
| 2 |
∴AN=NE=
| 1 |
| 2 |
∵∠MNE=∠CDE=90°,
∴MN∥CD,
∴
| NE |
| ED |
| MN |
| CD |
| 1 |
| 2 |
∵CD=4,
∴MN=2,
在RT△MND中,∵MN=2,DN=3,
∴DM=
| DN2+MN2 |
| 22+32 |
| 13 |
故答案为
| 13 |
看了 如图,边长为4正方形ABCD...的网友还看了以下:
一:在三角形ABC中,已知角A>角B>角>C,且角A=2倍角C,b=4,a+b=8,求a,c的长二 2020-05-20 …
已知△ABC中,a,b,c分别是角A.B.C所对的边,向量m→=(2sinB/2,√3/2).n→ 2020-05-22 …
15题.在三角形ABC中,角A,B,C对应的边长分别为a,b,c,且a=4,b=3,sin(A+C 2020-06-04 …
阅读下题的解题过程:已知a、b、c为三角形ABC的三边,且满足a^2c^2-b^2c^2=a^4- 2020-06-08 …
已知下列命题:1在△ABC中∠A=∠C-∠B则△ABC为直角三角形2在△ABC中若∠A:∠B:∠C 2020-07-04 …
s^1p^2组态的能量最低的光谱支项是()A、4^P1/21/2为P的下角标B.4^P5/2C、4 2020-07-09 …
规定一种新的运算:a三角形b等于a乘b减a加1,如3三角形4等于3乘4减3加1,请比较-3三角形2 2020-07-20 …
设三角形ABC的角A,B,C的对边分别是a,b,c且3b^2+3c^2-3a^2=4根号2bc求s 2020-07-20 …
1.在三角形abc中,证明a/b-b/a=c(CosB/b-CosA/a)2.在三角形abc中,已 2020-07-21 …
已知三角形ABC的三边a,b,c满足a^2c^2-b^2c^2=a^4-b^4,是判断三角形ABC的 2020-11-24 …