早教吧作业答案频道 -->数学-->
如图,已知在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,作∠DAF=90°,且AF=AD,过点F作EF∥AD,且EF=AF,联结CF,CE.(1)求证:FC⊥BC;(2)如果BD=AC,求证:点C在线段DE的垂直平分线上.
题目详情
如图,已知在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,作∠DAF=90°,且AF=AD,过点F作EF∥AD,且EF=AF,联结CF,CE.
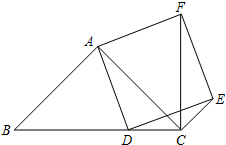
(1)求证:FC⊥BC;
(2)如果BD=AC,求证:点C在线段DE的垂直平分线上.

(1)求证:FC⊥BC;
(2)如果BD=AC,求证:点C在线段DE的垂直平分线上.
▼优质解答
答案和解析
(1)∵∠BAC=∠DAF=90°,
∴∠BAC-∠DAC=∠DAF-∠DAC,
即∠BAD=∠CAF,
又∵AB=AC,AD=AF,
∴△ABD≌△ACF,
∴∠B=∠ACF,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠ACF=∠B=45°,
∴∠BCF=90°,
∴FC⊥BC;
(2)∵△ABD≌△ACF,
∴BD=FC,
又∵BD=AC,
∴AC=FC,
∴∠CAF=∠CFA,
∵∠DAF=90°,EF∥AD,
∴∠DAF=∠AFE=90°,
∴∠DAC=∠EFC,
∵AD=AF,EF=AF,
∴AD=FE,
∴△ADC≌△FEC,
∴CD=CE,
∴点C在线段DE的垂直平分线上.
∴∠BAC-∠DAC=∠DAF-∠DAC,
即∠BAD=∠CAF,
又∵AB=AC,AD=AF,
∴△ABD≌△ACF,
∴∠B=∠ACF,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∴∠ACF=∠B=45°,
∴∠BCF=90°,
∴FC⊥BC;
(2)∵△ABD≌△ACF,
∴BD=FC,
又∵BD=AC,
∴AC=FC,
∴∠CAF=∠CFA,
∵∠DAF=90°,EF∥AD,
∴∠DAF=∠AFE=90°,
∴∠DAC=∠EFC,
∵AD=AF,EF=AF,
∴AD=FE,
∴△ADC≌△FEC,
∴CD=CE,
∴点C在线段DE的垂直平分线上.
看了 如图,已知在△ABC中,∠B...的网友还看了以下:
已知三角形ABC的三个顶点A(6,7)B(0,3)C(4,0)(1)求AC边上的中线所在直线方程; 2020-04-08 …
如图,点a,b在圆0上,ab=ac,角b0c=120度求证三角形abc的形状是等边三角形,求角c 2020-05-17 …
已知P(A)=P(B)=P(C)=0.25,P(AC)=0,P(AB)=P(AC)=0.15,则A 2020-06-04 …
1.如是B分之A>0,C分之B>0,那么AC()0;如果B分之A<0,C分之B<0,那么AC()0 2020-07-09 …
如图,过y轴上一点A(0,1)作AC平行于x轴,交抛物线如图,过y轴上一点A(0,1)作AC平行X 2020-07-29 …
如图,在平面直角坐标系中,点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D为A 2020-07-30 …
在等腰三角形ABC中,已知AB=AC,且点B(-1,0),点D(2,0)为AC的中点,(1)求点C 2020-07-30 …
已知三角形三个顶点的坐标.已知三角形三个顶点的坐标分别为A(4,1),B(0,3),C(2,4), 2020-08-01 …
根据条件:a、b、c满足c<b<a,且a+b+c=0,下列推理正确的是(填上序号)①ac(a-c)> 2020-12-05 …
在平面直角坐标系中,已知点A(-2,0),B(2,0),若在坐标轴上存在点C,使得AC+BC=m,则 2021-01-12 …