早教吧作业答案频道 -->数学-->
如图:已知∠AOB=30°,D是OA上一点,且OD=6cm,射线OC平分∠AOB,P、Q分别是射线OC、线段OA上的动点,则PQ+PD的最小值=.
题目详情
如图:已知∠AOB=30°,D是OA上一点,且OD=6cm,射线OC平分∠AOB,P、Q分别是射线OC、线段OA上的动点,则PQ+PD的最小值=___.
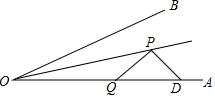

▼优质解答
答案和解析
如图,作点Q关于OC的对称点Q′,连接PQ′,作DQ″⊥OB于Q″交OC于P′.
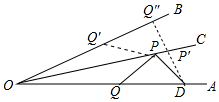
∵PQ+PD=PQ′+PD,
∴根据垂线段最短,当DQ″⊥OB时,PD+PQ的值最小,最小值为DP′+P′Q″=DQ″,
∵OD=6,∠DOQ″=30°,∠DQ″O=90°,
∴DQ″=
OD=3,
∴PQ+PD的最小值为3.
故答案为3.

∵PQ+PD=PQ′+PD,
∴根据垂线段最短,当DQ″⊥OB时,PD+PQ的值最小,最小值为DP′+P′Q″=DQ″,
∵OD=6,∠DOQ″=30°,∠DQ″O=90°,
∴DQ″=
| 1 |
| 2 |
∴PQ+PD的最小值为3.
故答案为3.
看了 如图:已知∠AOB=30°,...的网友还看了以下:
初三数学,急用,今天1、已知⊙O的直径为6,P为直线L上一点,OP=3那么直线L与⊙O的位置关系是 2020-04-26 …
已知cosO=-3/5,O属于(/2,),求sin(O+/3)的值已知sinO=-12/13,O是 2020-05-13 …
(2014•玉林)如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O 2020-07-11 …
数学的贝克莱悖论如何解决的?当x增长为x+o时,x的立方(记为x^3)成为(x+o)的立方(记为( 2020-07-24 …
1.在△ABC中,已知AB=1,AC=3,点H,O分别是△ABC的垂心和外心,则向量HO*向量BC 2020-07-30 …
如图,已知⊙O的半径为2,以⊙O的弦AB为直径作⊙M,点C是⊙O优弧AB上的一个动点,(不与点A、 2020-07-31 …
如图,在平面直角坐标系中,已知正方形OABC的顶点坐标分别为O(0,0),A(3,0),B(3,3 2020-08-02 …
已知⊙O与⊙O′内切于点A,⊙O的弦BC与⊙O′切于点D,AB、AC与⊙O′分别交于点E、F,AG、 2020-12-01 …
如图,已知⊙O和⊙O′相交于A、B两点,过点A作⊙O′的切线交⊙O于点C,过点B作两圆的割线分别交⊙ 2020-12-05 …
在平面直角坐标系中,已知直线AB:y=-¾+3分别与x轴、y轴分别交于点A、点B.动点P、Q分别从O 2021-01-12 …