早教吧作业答案频道 -->数学-->
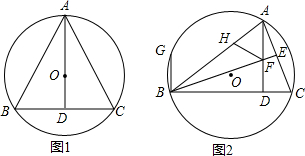
已知锐角三角形ABC内接于O,AD⊥BC.垂足为D.(1)如图1,若AB=BC,BD=DC,求∠B的度数.(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交O于点G,在AB边上取一点H,使得AH=BG;求证
题目详情
已知锐角三角形ABC内接于 O,AD⊥BC.垂足为D.
(1)如图1,若
=
,BD=DC,求∠B的度数.
(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交 O于点G,在AB边上取一点H,使得AH=BG;求证:△AFH是等腰三角形.
(1)如图1,若
 |
| AB |
 |
| BC |
(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交 O于点G,在AB边上取一点H,使得AH=BG;求证:△AFH是等腰三角形.

▼优质解答
答案和解析
(1)∵
=
,
∴AB=BC.
∵AD⊥BC,BD=DC,
∴AD是线段BC的垂直平分线,
∴AB=AC,
∴△ABC是等边三角形,
∴∠B=60°;
(2)连接GC,GA,
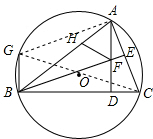 ∵BG⊥BC,
∵BG⊥BC,
∴GC是 O的直径,
∴∠GAC=90°.
∵BE⊥AC,
∴∠BEC=∠GAC=90°,
∴AG∥BE.
∵AD⊥BC,
∴∠ADC=∠GBC=90°,
∴BG∥AD,
∴四边形GBFA是平行四边形,
∴BG=AF.
∵BG=AH,
∴AH=AF,
∴△AFH是等腰三角形.
 |
| AB |
 |
| BC |
∴AB=BC.
∵AD⊥BC,BD=DC,
∴AD是线段BC的垂直平分线,
∴AB=AC,
∴△ABC是等边三角形,
∴∠B=60°;
(2)连接GC,GA,
 ∵BG⊥BC,
∵BG⊥BC,∴GC是 O的直径,
∴∠GAC=90°.
∵BE⊥AC,
∴∠BEC=∠GAC=90°,
∴AG∥BE.
∵AD⊥BC,
∴∠ADC=∠GBC=90°,
∴BG∥AD,
∴四边形GBFA是平行四边形,
∴BG=AF.
∵BG=AH,
∴AH=AF,
∴△AFH是等腰三角形.
看了 已知锐角三角形ABC内接于O...的网友还看了以下:
有理数a,b在数轴上的对应点如图所示,则下面式子中正确的是()A.b>a>0B.a>b>0C.a+ 2020-05-13 …
a,b是有理数,它们在数轴上的对应点的位置如下图所示,把a,-a,b,-b,a+b,a-b按照从小 2020-05-13 …
如图所示,若悬绳A和弹簧秤B的重力不计,下列各对力中属于平衡力的是()A.A对B的拉力与B对C的拉 2020-06-26 …
下列测定Na2CO3和NaOH混合物中Na2CO3质量分数的实验方案中,不严密的是()A.取a克混 2020-07-08 …
如图所示,一固定光滑足够长斜面AB的倾角θ=30°,一小物块以大小v0=4m/s的初速度从斜面底端 2020-07-13 …
如图中,弹簧固定在天花板A上,下端悬挂物体C,弹簧自重不计,下列各对力中属于平衡力的是()A.A对 2020-07-21 …
A、B、C都是金属,把A、B组成原电池时,A为负极;把B放入C的盐溶液中,B的表面附着一层金属C. 2020-07-29 …
a.b.c是正数求函数y=根号下(x^2+a^2)+根号下[(c-x)^2+b^2]最小值书上说用 2020-08-02 …
下列能保证a⊥∂(a,b,c为直线,∂为平面)的条件是()A.b,c⊂∂.a⊥b,a⊥cB.b,c⊂ 2020-11-02 …
设A,B,A+B均可逆,则(A-1+B-1)-1等于()A.A-1+B-1B.A+BC.B(A+B) 2020-11-03 …