早教吧作业答案频道 -->数学-->
已知抛物线y=x2+h与x轴交于A、B两点,与y轴交于C点,且OC=AB.(1)求此抛物线的解析式;(2)直线y=2x+b被抛物线截得线段长为230,求b.
题目详情
已知抛物线y=x2+h与x轴交于A、B两点,与y轴交于C点,且OC=AB.
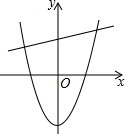
(1)求此抛物线的解析式;
(2)直线y=2x+b被抛物线截得线段长为2
,求b.

(1)求此抛物线的解析式;
(2)直线y=2x+b被抛物线截得线段长为2
| 30 |
▼优质解答
答案和解析
(1)如图由题意,OA=OB,

∵OC=AB,
∴OA=OB=-
h,
∴点B坐标(-
h,0),
把点B坐标代入y=x2+h得到,0=
h2+h,解得h=-4或0(舍弃),
∴抛物线的解析式为y=x2-4.
(2)设直线y=2x+b与抛物线y=x2-4的交点为E(x1,y1),F(x2,y2).
由
消去y得到x2-2x-4-b=0,
∴x1+x2=2,x1x2=-4-b,由此可得y1+y2=4+2b,y1y2=b2-16,
∴(x1-x2)2=(x1+x2)2-4x1x2=4b+20,同理可得(y1-y2)2=16b+80,
∵EF=2
,
∴4b+20+16b+80=120,
∴b=1.

∵OC=AB,
∴OA=OB=-
| 1 |
| 2 |
∴点B坐标(-
| 1 |
| 2 |
把点B坐标代入y=x2+h得到,0=
| 1 |
| 4 |
∴抛物线的解析式为y=x2-4.
(2)设直线y=2x+b与抛物线y=x2-4的交点为E(x1,y1),F(x2,y2).
由
|
∴x1+x2=2,x1x2=-4-b,由此可得y1+y2=4+2b,y1y2=b2-16,
∴(x1-x2)2=(x1+x2)2-4x1x2=4b+20,同理可得(y1-y2)2=16b+80,
∵EF=2
| 30 |
∴4b+20+16b+80=120,
∴b=1.
看了 已知抛物线y=x2+h与x轴...的网友还看了以下:
设非空集合A={X/-2≤x≤a},B={y/y=2x+3,x∈A},C={Z/Z=X^2,x∈A 2020-04-06 …
已知集合A={x|-2≤x≤a},B={y|y=2x+3,x∈A},C={z|z=x^2,x∈A} 2020-04-06 …
集合A={x|-2≤x≤a},B={y|y=2x+3,x∈A},C={y|y=x2,x∈A},且C 2020-05-15 …
集合A={x|-2≤x≤a},B={y|y=2x+3,x∈A},C={y=x²,x∈A}且C包含于 2020-05-15 …
已知x=a/(b+c),y=b/(c+a),z=c/(a+b),且a+b+c不等于0,求x/(1+ 2020-06-06 …
在平面直角坐标系中,直线L1:y=2x+b交x轴正半轴于点A,点B(4,0)在点A的右边,现过点B 2020-06-14 …
1.已知集合A={x│-2≤x≤a,a〉-2},B={y│y=2x+3,x属于A},C={z│z= 2020-07-18 …
1.A={x|x²+4x=0}B={x|x²+2(a+1)x+a²-1=0,a∈R,x∈R},若A∪ 2020-11-01 …
多元一次方程求解A*B*C*D*E*F*G*H*M*N*X*Y不等于0,且全是大于0的正整数4A=A 2020-12-14 …
一道数学难题,有两个直线L1:x/a+y/b=1L2:x/c+y/d=1设其交点为P为甚么x(1/a 2020-12-24 …