早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的O经过AB的中点E,交AD的延长线于点F,连结EF.(1)求证:∠1=∠F.(2)若sinB=55,EF=25,求CD的长.
题目详情
如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的 O经过AB的中点E,交AD的延长线于点F,连结EF.
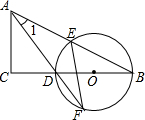
(1)求证:∠1=∠F.
(2)若sinB=
,EF=2
,求CD的长.

(1)求证:∠1=∠F.
(2)若sinB=
| ||
| 5 |
| 5 |
▼优质解答
答案和解析
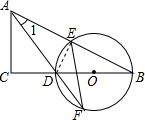 (1)证明:连接DE,
(1)证明:连接DE,
∵BD是 O的直径,
∴∠DEB=90°,
∵E是AB的中点,
∴DA=DB,
∴∠1=∠B,
∵∠B=∠F,
∴∠1=∠F;
(2)∵∠1=∠F,
∴AE=EF=2
,
∴AB=2AE=4
,
在Rt△ABC中,AC=AB•sinB=4,
∴BC=
=8,
设CD=x,则AD=BD=8-x,
∵AC2+CD2=AD2,
即42+x2=(8-x)2,
∴x=3,即CD=3.
 (1)证明:连接DE,
(1)证明:连接DE,∵BD是 O的直径,
∴∠DEB=90°,
∵E是AB的中点,
∴DA=DB,
∴∠1=∠B,
∵∠B=∠F,
∴∠1=∠F;
(2)∵∠1=∠F,
∴AE=EF=2
| 5 |
∴AB=2AE=4
| 5 |
在Rt△ABC中,AC=AB•sinB=4,
∴BC=
| AB2-AC2 |
设CD=x,则AD=BD=8-x,
∵AC2+CD2=AD2,
即42+x2=(8-x)2,
∴x=3,即CD=3.
看了 如图,在△ABC中,∠C=9...的网友还看了以下:
已知正方形的边长为10,EC=3,BF=2,则S四边形ABCD=.没有图,只能大概描述一下,点E和 2020-05-13 …
初三二次根式与一元二次方程问题如图,将边长为3+√3的等边△ABC折叠,折痕为DE,点B与点F重合 2020-05-15 …
如图,在正方体ABCD-A′B′C′D′中,点E在A′B上,点F在B′D′上,且BE=BF,求证: 2020-05-16 …
(2012•南开区一模)如图,将边长为3+3的等边△ABC折叠,折痕为DE,点B与点F重合,EF和 2020-07-19 …
如图,已知双曲线x2a2-y2b2=1(a>0,b>0)上有一点A,它关于原点的对称点为B,点F为 2020-07-26 …
如图所示,将矩形ABCD折叠,使点B落在边AD上,点B与点F重合,折痕为AE,此时,矩形ECDF与 2020-07-31 …
如图,四边形ABCD与四边形CEFH均为正方形,点B、C、E在同一直线上,连接BD,DF,BF.( 2020-08-02 …
(2004•南平)如图1,正方形ABCD的边长为2厘米,点E从点A开始沿AB边移动到点B,点F从点B 2020-11-12 …
直角三角形ABC中,∠ACB=90°,直线l过点C.(1)当AC=BC时,如图1,分别过点A和B作A 2020-12-05 …
如图,把矩形ABCD中的AB边向上翻折到AD边上,当点B与点F重合时,折痕与BC边交于点E,连接EF 2020-12-15 …