如图，矩形EFGH的四个顶点分别在菱形ABCD的四条边上，BE=BF，将△AEH，△CFG分别沿边EH，FG折叠，当重叠部分为菱形且面积是菱形ABCD面积的116时，则AEEB为（）A.53B.2C.52D.4

Question

如图，矩形EFGH的四个顶点分别在菱形ABCD的四条边上，BE=BF，将△AEH，△CFG分别沿边EH，FG折叠，当重叠部分为菱形且面积是菱形ABCD面积的

(1)/(16)时，则(AE)/(EB)为（　　）

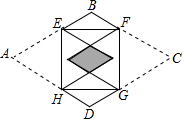
A.

(5)/(3)

B. 2

C.

(5)/(2)

D. 4

Answer 1

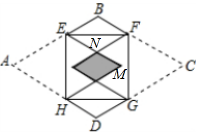设重叠的菱形边长为x，BE=BF=y，
由矩形和菱形的对称性以及折叠的性质得：四边形AHME、四边形BENF是菱形，
∴AE=EM，EN=BE=y，EM=x+y，
∵当重叠部分为菱形且面积是菱形ABCD面积的(1)/(16)，且两个菱形相似，
∴AB=4MN=4x，
∴AE=AB-BE=4x-y，
∴4x-y=x+y，
解得：x=(2)/(3)y，
∴AE=(5)/(3)y，
∴(AE)/(EB)=((5)/(3)y)/(y)=(5)/(3)；
故选：A．