早教吧作业答案频道 -->数学-->
我们学习了锐角三角函数的相关知识,知道锐角三角函数定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长的比与
题目详情
我们学习了锐角三角函数的相关知识,知道锐角三角函数定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长的比与角的大小之间可以相互转化.如图1,在Rt△ABC中,∠C=90°.若∠A=30°,则cosA=
=
=
.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对.如图2,在△ABC中,AB=AC,顶角A的正对记作sadA,这时,sadA=
=
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述角的正对的定义,解答下列问题:
(1)直接写出sad60°的值为___;
(2)若0°<∠A<180°,则∠A的正对值sad A的取值范围是___;
(3)如图2,已知tanA=
,其中∠A为锐角,求sadA的值;
(4)直接写出sad36°的值为___.
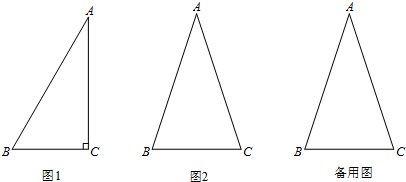
| ∠A 的邻边 |
| 斜边 |
| AC |
| AB |
| ||
| 2 |
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对.如图2,在△ABC中,AB=AC,顶角A的正对记作sadA,这时,sadA=
| 底边 |
| 腰 |
| BC |
| AB |
根据上述角的正对的定义,解答下列问题:
(1)直接写出sad60°的值为___;
(2)若0°<∠A<180°,则∠A的正对值sad A的取值范围是___;
(3)如图2,已知tanA=
| 3 |
| 4 |
(4)直接写出sad36°的值为___.

▼优质解答
答案和解析
(1)根据正对定义,
当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,
则sad60°=
=1.
故答案为:1;
(2)当∠A接近0°时,sadA接近0,
当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadA接近2.
于是sadA的取值范围是0<sadA<2.
故答案为:0<sadA<2.
(3)如图2,过点B作BD⊥AC于点D.
∴∠ADB=∠CDB=90°.

在Rt△ADB中,tanA=
,
∴设BD=3k,则AD=4k.
∴AB=
=5k.
∵AB=AC,
∴CD=k.
∴在Rt△CDB中,利用勾股定理得,BC=
k.
在等腰△ABC中,sad A=
=
=
.
(4)如图3所示:已知:∠A=36°,AB=AC,BC=BD,
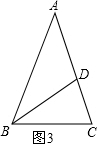
∴∠A=∠CBD=36°,∠ABC=∠C=72°,
∴△BCD∽△ABC,
∴
=
,
∴
=
,
解得:BC=
CD,
∴sad36°=
=
.
故答案为:
.
当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,
则sad60°=
| 1 |
| 1 |
故答案为:1;
(2)当∠A接近0°时,sadA接近0,
当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadA接近2.
于是sadA的取值范围是0<sadA<2.
故答案为:0<sadA<2.
(3)如图2,过点B作BD⊥AC于点D.
∴∠ADB=∠CDB=90°.

在Rt△ADB中,tanA=
| 3 |
| 4 |
∴设BD=3k,则AD=4k.
∴AB=
| BD2+AD2 |
∵AB=AC,
∴CD=k.
∴在Rt△CDB中,利用勾股定理得,BC=
| 10 |
在等腰△ABC中,sad A=
| BC |
| AB |
| ||
| 5k |
| ||
| 5 |
(4)如图3所示:已知:∠A=36°,AB=AC,BC=BD,

∴∠A=∠CBD=36°,∠ABC=∠C=72°,
∴△BCD∽△ABC,
∴
| BC |
| AC |
| CD |
| BC |
∴
| BC |
| BC+CD |
| CD |
| BC |
解得:BC=
| ||
| 2 |
∴sad36°=
| CD |
| BC |
| ||
| 2 |
故答案为:
| ||
| 2 |
看了 我们学习了锐角三角函数的相关...的网友还看了以下:
一个三角形的三个内角的度数比是1:2:3,这个三角形是()三角形?说清楚是什么三角形?锐角?直角? 2020-05-14 …
三角形ABC的三个内角的Sin值与三角形A'B'C'的Cos值相等请问这2个三角形分别是什么三角形 2020-05-14 …
因式分解,多边形,相似三角形,二次函数,反比例函数,扇形,锐角三角形,解直角三角形.谢 2020-05-16 …
所有三角形的各个角的度数等边三角形等腰三角形矩形梯形平行四边形菱形锐角、钝角越全越好谢求各个三角形 2020-06-03 …
三角形有两个内角的差恰好等于90那么这个三角形是钝角三角形锐角三角形直角三角形锐角或钝角三角形 2020-06-04 …
一个等腰直角三角形在一个平面内的正投影可能是.(把你认为正确的选项的代号都填上)①等腰直角三角形② 2020-06-08 …
等腰三角形可能是锐角三角形,也可能是钝角形对吗.三角形按角分可分为直角三角形锐角三角形和钝角三角形 2020-07-30 …
三角形分为:直角三角形锐角三角形和钝角三角形.那么什么样的三角形叫直角三角形? 2020-07-30 …
已知直角三角形一个尖角度数和直边长度求另一直边长度已知直角三角形锐角是2.5°锐角对面的直边是17 2020-08-02 …
三角形角2平分线夹角与顶角的关系具体分类讨论1内角平分线1外角平分线,2外角平分线,2内角平分线( 2020-08-03 …