早教吧作业答案频道 -->数学-->
如图1,△ABC中,AB=AC,∠BAC=90°,直线l经过点A,过B、C两点分别作直线l的垂线段,垂足分别为D、E.(1)求证:AE=BD;(2)点O为BC的中点,连接DO、EO,如图2,试判断△ODE的形状?并说明理
题目详情
如图1,△ABC中,AB=AC,∠BAC=90°,直线l经过点A,过B、C两点分别作直线l的垂线段,垂足分别为D、E.
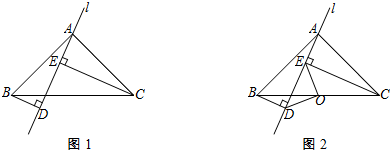
(1)求证:AE=BD;
(2)点O为BC的中点,连接DO、EO,如图2,试判断△ODE的形状?并说明理由.

(1)求证:AE=BD;
(2)点O为BC的中点,连接DO、EO,如图2,试判断△ODE的形状?并说明理由.
▼优质解答
答案和解析
(1)证明:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵CE⊥直线l,
∴∠ACE+∠CAE=90°,
∴∠BAD=∠ACE,
∵BD⊥直线l,CE⊥直线l,
∴∠ADB=∠CEA=90°,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴AE=BD;
(2)△ODE是等腰直角三角形.
理由如下:如图,连接AO,
∵AB=AC,∠BAC=90°,点O为BC的中点,
∴AO=BO,∠CAO=45°,∠AOB=90°,
∵△ABD≌△CAE,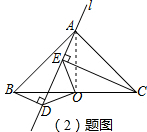
∴∠ABD=∠CAE,
∴∠ABD-∠ABO=∠CAE-∠CAO,
∵∠ABO=∠CAO=45°,
∴∠OAE=∠OBD,
在△AOE和△BOD中,
,
∴△AOE≌△BOD(SAS),
∴OE=OD,∠AOE=∠BOD,
∴∠DOE=∠BOE+∠BOD=∠BOE+∠AOE=∠AOB=90°,
∴△ODE是等腰直角三角形.
∴∠BAD+∠CAE=90°,
∵CE⊥直线l,
∴∠ACE+∠CAE=90°,
∴∠BAD=∠ACE,
∵BD⊥直线l,CE⊥直线l,
∴∠ADB=∠CEA=90°,
在△ABD和△CAE中,
|
∴△ABD≌△CAE(AAS),
∴AE=BD;
(2)△ODE是等腰直角三角形.
理由如下:如图,连接AO,
∵AB=AC,∠BAC=90°,点O为BC的中点,
∴AO=BO,∠CAO=45°,∠AOB=90°,
∵△ABD≌△CAE,

∴∠ABD=∠CAE,
∴∠ABD-∠ABO=∠CAE-∠CAO,
∵∠ABO=∠CAO=45°,
∴∠OAE=∠OBD,
在△AOE和△BOD中,
|
∴△AOE≌△BOD(SAS),
∴OE=OD,∠AOE=∠BOD,
∴∠DOE=∠BOE+∠BOD=∠BOE+∠AOE=∠AOB=90°,
∴△ODE是等腰直角三角形.
看了 如图1,△ABC中,AB=A...的网友还看了以下:
在平面直角坐标系中,用线段顺次连接点(-2,0)(0,3)(3,3)在平面直角坐标系中,用线段依次 2020-04-07 …
在直角坐标系中,用线段顺次连接A(-2,0),B(0,3),C(3,0),D(4,0).(1)这是 2020-05-14 …
在直角坐标系中,用线段顺次连接A(-2,0),B(0,3),C(3,3),D(4,0).(1)这是 2020-05-14 …
请问求原点到曲面在z^2=xy+x-y+4的最短距离,建立方程L(x,y,z,c)=(x^2+y^ 2020-05-16 …
给出定理“圆内接四边形的对角互补”,根据定理求k为何值时,直线l:x+3y-7=0和l:kx-y- 2020-05-17 …
个关于数学里直线方程式的问题-.1.求过点P,且平行于直线L的直线方程(1)P(5.2)L:3X- 2020-06-03 …
下列原电池中,电动势最大的是:A,(-)Zn/Zn^2+(1mol/L)//Ag+(1mol/L) 2020-07-01 …
判断下列各对直线是否垂直:(1)y=x,2x+2y-7=0(2)x+4y-5=0,4x-3y-5= 2020-08-01 …
表格公式ROUND(T5+W5+X5+Y5+Z5+AA5+AB5+AC5+AD5-$L$2*0.8/ 2020-10-31 …
(2014•唐山一模)如图所示,电源电动势E=3V,小灯泡L标有“2V、0.4W”,开关S接l,当变 2020-11-12 …