早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过点D作DE⊥AC于E.(1)求证:∠CBP=∠ABP;(2)若AB-BC=4,AC=8.①求AB的长度及△ABP的面积;②求AE的长
题目详情
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过点D作DE⊥AC于E.
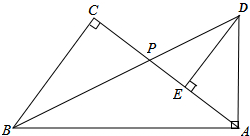
(1)求证:∠CBP=∠ABP;
(2)若AB-BC=4,AC=8.
①求AB的长度及△ABP的面积;
②求AE的长.

(1)求证:∠CBP=∠ABP;
(2)若AB-BC=4,AC=8.
①求AB的长度及△ABP的面积;
②求AE的长.
▼优质解答
答案和解析
(1)∵∠C=90°,
∴∠CBP+∠BPC=90°,
∵DA⊥BA,
∴∠PBA+∠BDA=90°,
∵AD=AP,
∴∠BDA=∠DPA=∠BPC,
∠CBP=∠ABP;
(2)①设AB=x,
∵AB-BC=4,
∴BC=x-4,
∵AC=8,
∴在Rt△ABC中,(x-4)2+64=x2,
解得:x=10,
即AB=10,
∴BC=6,
过点P作PF⊥BA于点F,如图,

在△BCP和△BFP中:
,
∴△BCP≌△BFP(AAS),
∴BF=BC=6,PF=PC,
∴AF=4,
设PF=PC=y,
在Rt△PAF中,16+y2=(8-y)2,
解得:y═3,
即PF=3,
∴S△ABP=
×AB×PF=
×10×3=15;
③∵DE⊥AC,
∴∠EAD+∠ADE=90°=∠PAF+∠EAD,
∠PAF=∠ADE,
在△PAF和△ADE中,
,
∴△PAF≌△ADE(AAS),
∴AE=PF=3.
∴∠CBP+∠BPC=90°,
∵DA⊥BA,
∴∠PBA+∠BDA=90°,
∵AD=AP,
∴∠BDA=∠DPA=∠BPC,
∠CBP=∠ABP;
(2)①设AB=x,
∵AB-BC=4,
∴BC=x-4,
∵AC=8,
∴在Rt△ABC中,(x-4)2+64=x2,
解得:x=10,
即AB=10,
∴BC=6,
过点P作PF⊥BA于点F,如图,

在△BCP和△BFP中:
|
∴△BCP≌△BFP(AAS),
∴BF=BC=6,PF=PC,
∴AF=4,
设PF=PC=y,
在Rt△PAF中,16+y2=(8-y)2,
解得:y═3,
即PF=3,
∴S△ABP=
| 1 |
| 2 |
| 1 |
| 2 |
③∵DE⊥AC,
∴∠EAD+∠ADE=90°=∠PAF+∠EAD,
∠PAF=∠ADE,
在△PAF和△ADE中,
|
∴△PAF≌△ADE(AAS),
∴AE=PF=3.
看了 如图,在Rt△ABC中,∠C...的网友还看了以下:
在矩形ABCD中,AB=2,AD=3,点P在边AD上,连接BP,点A关于直线BP为对称点为A1(1 2020-05-16 …
等边三角形ABC的边长1,P为AB上的一个动点(不包括A、B),PQ垂直BC,QR垂直AC,RS垂 2020-06-02 …
菱形ABCD中,点P为CD上一点,连接BP.(1)如图1,若BP⊥CD,菱形ABCD边长为10,P 2020-07-09 …
求某一点的轨迹方程已知点A(-2,0),动点P在曲线y=2x^2上运动,又一点B在线段AP的延长线 2020-07-13 …
如图,平行四边形abcd中,p是cd上的一点,且ap和bp分别平分角dab和角cba.1.求角ap 2020-07-24 …
1.已知AB=8,点P是线段AB的黄金分割点,且AP>BP,求:(1)BP的长;(2)AP-BP的 2020-07-24 …
如图,在三角形ABC中,角C=90°,P为AB上一点,且点P不与点A重合,过点P作PE垂直AB交A 2020-08-03 …
如图,P是O外一点,OP交O于点A,OA=AP.甲、乙两人想作一条通过点P与O相切的直线,其作法如下 2020-11-02 …
等边三角形abc,边长为x.过点a做垂直于平面abc的线段ap.长度为2x.求角abp和角pbc各为 2020-11-04 …
在矩形ABCD中,点P是边AD上的动点,联结BP,线段BP的垂直平分线交边BC于点Q,垂足为点M,联 2020-12-07 …