分子式与苯丙氨酸()相同，且同时符合下列两个条件：①有带两个取代基的苯环；②有一个硝基直接连接在苯环上。那么，这种物质的异构体的数目是()A．

Question

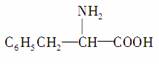分子式与苯丙氨酸 ( ) 相

同，且同时符合下列两个条件： ① 有带两个取代基的苯环； ② 有一个硝基直接连接在苯环上。那么，这种物质的异构体的数目是 ( 　　 )

A ． 3 种                  B ． 5 种

C ． 6 种                  D ． 10 种

分子式与苯丙氨酸 ( 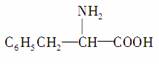) 相

同，且同时符合下列两个条件： ① 有带两个取代基的苯环； ② 有一个硝基直接连接在苯环上。那么，这种物质的异构体的数目是 ( 　　 )

A ． 3 种                  B ． 5 种

C ． 6 种                  D ． 10 种

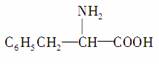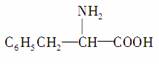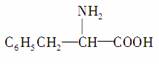分子式与苯丙氨酸 ( ) 相

( ) 相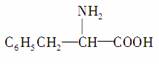 ) 相 ) 相

同，且同时符合下列两个条件： ① 有带两个取代基的苯环； ② 有一个硝基直接连接在苯环上。那么，这种物质的异构体的数目是 ( 　　 )

① 有带两个取代基的苯环； ② 有一个硝基直接连接在苯环上。那么，这种物质的异构体的数目是 ( 　　 ) ② 有一个硝基直接连接在苯环上。那么，这种物质的异构体的数目是 ( 　　 ) ( 　　 ) )

A ． 3 种                  B ． 5 种

A ． 3 种                  B ． 5 种 3 种                  B ． 5 种                  B ． 5 种 5 种

C ． 6 种                  D ． 10 种

C ． 6 种                  D ． 10 种 6 种                  D ． 10 种                  D ． 10 种 10 种

Answer 1

C 　 [ 氨基酸与同碳硝基化合物互为同分异构体，据题意苯环上有一个 —NO ₂ ，另一个基团则为正丙基或异丙基，分别有邻、间、对三种同分异构体，共 2×3 ＝ 6 种。 ]

C 　 [ 氨基酸与同碳硝基化合物互为同分异构体，据题意苯环上有一个 —NO ₂ ，另一个基团则为正丙基或异丙基，分别有邻、间、对三种同分异构体，共 2×3 ＝ 6 种。 ]

C 　 [ 氨基酸与同碳硝基化合物互为同分异构体，据题意苯环上有一个 —NO ₂ 2 ，另一个基团则为正丙基或异丙基，分别有邻、间、对三种同分异构体，共 2×3 ＝ 6 种。 ]