早教吧作业答案频道 -->数学-->
如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.(1)证明△BCM≌△CAN;(2)∠AEM=°;(3)求证DE平分∠AEC;(4)试猜想AE,CE,DE之间的
题目详情
如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.
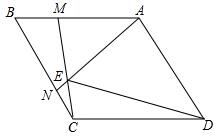
(1)证明△BCM≌△CAN;
(2)∠AEM=___°;
(3)求证DE平分∠AEC;
(4)试猜想AE,CE,DE之间的数量关系并证明.

(1)证明△BCM≌△CAN;
(2)∠AEM=___°;
(3)求证DE平分∠AEC;
(4)试猜想AE,CE,DE之间的数量关系并证明.
▼优质解答
答案和解析
(1)如图1中,连接AC.
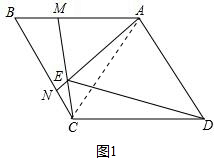
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠ADC=60°,
∴△ACD,△ABC是等边三角形,
∴BC=AC,∠B=∠ACN=60°,
在△BCM和△CAN中,
,
∴△BCM≌△CAN.
(2)如图1中,∵△BCM≌△CAN,
∴∠BCM=∠CAN,
∴AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°.
故答案为60.
(3)如图2中,作DG⊥AN于G.DH⊥MC交MC的延长线于H.
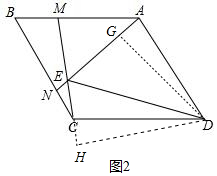
∵∠AEM=60°,
∴∠AEC=120°,
∵∠DGE=∠H=90°,
∴∠GEH+∠GDH=180°,
∴∠GDH=∠ADC=60°,
∴∠ADG=∠CDH,
在△DGA和△DHC中,
,
∴△DGA≌△DHC,
∴DG=DH,
∵DG⊥AN,DH⊥MC,
∴∠DEG=∠DEH.
∴DE平分∠AEC.
(4)结论:EA+EC=ED.理由如下:
如图2中,由(3)可知,∠GED=60°,
在Rt△DEG中,∵∠EDG=30°,
∴DE=2EG,
易知△DEG≌△DEH,
∴EG=EH,
∴EA+EC=EG+AG+EH-CH,
∵△DGA≌△DHC,
∴GA=CH,
∴EA+EC=2EG=DE,
∴EA+EC=ED.

∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠ADC=60°,
∴△ACD,△ABC是等边三角形,
∴BC=AC,∠B=∠ACN=60°,
在△BCM和△CAN中,
|
∴△BCM≌△CAN.
(2)如图1中,∵△BCM≌△CAN,
∴∠BCM=∠CAN,
∴AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°.
故答案为60.
(3)如图2中,作DG⊥AN于G.DH⊥MC交MC的延长线于H.

∵∠AEM=60°,
∴∠AEC=120°,
∵∠DGE=∠H=90°,
∴∠GEH+∠GDH=180°,
∴∠GDH=∠ADC=60°,
∴∠ADG=∠CDH,
在△DGA和△DHC中,
|
∴△DGA≌△DHC,
∴DG=DH,
∵DG⊥AN,DH⊥MC,
∴∠DEG=∠DEH.
∴DE平分∠AEC.
(4)结论:EA+EC=ED.理由如下:
如图2中,由(3)可知,∠GED=60°,
在Rt△DEG中,∵∠EDG=30°,
∴DE=2EG,
易知△DEG≌△DEH,
∴EG=EH,
∴EA+EC=EG+AG+EH-CH,
∵△DGA≌△DHC,
∴GA=CH,
∴EA+EC=2EG=DE,
∴EA+EC=ED.
看了 如图菱形ABCD中,∠ADC...的网友还看了以下:
几道因式分解1.说明(a2+3a)(a2+3a+2)+1是一个完全平方公式.2.设n为大于1正整数 2020-04-10 …
已知2mx-y-8m+3=0,圆c:x^2+y^2-6x-12y+20=0,(1)M∈R,证明:l 2020-05-21 …
已知函数f(x)=(lnx)/x的图像为曲线C,函数g(x)=1/2*a*x+b的图像为直线l.( 2020-06-04 …
(2014•龙东地区)已知△ABC中,M为BC的中点,直线m绕点A旋转,过B、M、C分别作BD⊥m 2020-06-15 …
超难证明题求证:C(n,k)+C(n,k-1)C(m,1)+C(n,k-2)C(m,2)+.+C( 2020-07-20 …
一个关于组合的证明题——证明:C(n+m,r)=C(n,0)C(m,r)+C(n,1)C(m,r- 2020-08-01 …
证明:若a,b,c都是奇数,则二次方程ax^2+bx+c=0没有有理数根它的解答的前两步是这样的: 2020-08-02 …
证明nC0+(n+1)C1+(n+2)C2+……+(n+m-1)C(m-1)=(n+m)C(m-1) 2020-10-31 …
证明组合性质:C(n+1,m)=C(n,m)+C(n,m-1)C(n+1,m)=(n+1)!/m!( 2020-11-01 …
1.若P(a,b)、Q(c,d)都在直线y=mx+k上,则PQ的绝对值用a、c、m表示为().A.( 2020-12-31 …