早教吧作业答案频道 -->数学-->
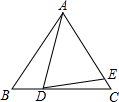
如图，在△ABC中，AB=AC，AD=DE，若∠BAD=18°，∠EDC=12°，则∠ADE=（）A、56°B、58°C、60°D、62°
题目详情
如图，在△ABC中，AB=AC，AD=DE，若∠BAD=18°，∠EDC=12°，则∠ADE=（ ）| A、56° | B、58° |
| C、60° | D、62° |
▼优质解答
答案和解析
考点：
等腰三角形的性质
专题：
分析：
设∠ADE=x°，则∠B+18°=x°+12°，可用x表示出∠B和∠C，再利用外角的性质可表示出∠DAE和∠DEA，在△ADE中利用三角形内角和可求得x．
设∠ADE=x°，且∠BAD=18°，∠EDC=12°，∴∠B+18°=x°+12°，∴∠B=x°-6°，∵AB=AC，∴∠C=∠B=x°-6°，∴∠DEA=∠C+∠EDC=x°-6°+12°=x°+6°，∵AD=DE，∴∠DEA=∠DAE=x°+6°，在△ADE中，由三角形内角和定理可得x+x+6+x+6=180，解得x=56，即∠ADE=56°，故选A．
点评：
本题主要考查等腰三角形的性质及外角的性质，用∠ADE表示出∠DAE和∠DEA是解题的关键．
考点：
等腰三角形的性质
专题：
分析：
设∠ADE=x°，则∠B+18°=x°+12°，可用x表示出∠B和∠C，再利用外角的性质可表示出∠DAE和∠DEA，在△ADE中利用三角形内角和可求得x．
设∠ADE=x°，且∠BAD=18°，∠EDC=12°，∴∠B+18°=x°+12°，∴∠B=x°-6°，∵AB=AC，∴∠C=∠B=x°-6°，∴∠DEA=∠C+∠EDC=x°-6°+12°=x°+6°，∵AD=DE，∴∠DEA=∠DAE=x°+6°，在△ADE中，由三角形内角和定理可得x+x+6+x+6=180，解得x=56，即∠ADE=56°，故选A．
点评：
本题主要考查等腰三角形的性质及外角的性质，用∠ADE表示出∠DAE和∠DEA是解题的关键．
看了 如图，在△ABC中，AB=A...的网友还看了以下：
求证:√2不是有理数?假设√2是有理数则√2可以写成一个最简分数假设是p/q=√2,p和q互质平方 2020-04-09 …
若关于x的分式方程（x-a）/（x-1） -3/x=1无解,则a=两边乘x(x-1)x(x-a)- 2020-05-15 …
高一复合函数f(2x+1)=x^2-2x,则f(2)=若f(x)+2f(1/x)=3x,则f（2） 2020-05-17 …
概率小问题几个,1:某运动员投篮的命中率为0.6,则投篮10次,恰投中2次的概率为?2:若ξ≈π（ 2020-07-09 …
等比数列{an}的前n项和Sn=2^n-1,则a1^2+a2^2+a3^2+...+an^2=前n 2020-07-30 …
若x-y=2,x^2+y^2=3,则m的值为（1）x-y=2,x^2+y^2=3,则xy的值为（2 2020-07-30 …
N道初二因式分解1.4x^4-a^2-6a-9=()^2-()^22.若2^n-1/2^n=6,则4 2020-11-03 …
若a(a-1)-(a^2-b)=7,则a^2+b^2)/2-ab=?若a(a-1)-(a²-b)=7 2020-11-07 …
(14)若(2x-3)(x+5)=ax^2+bx+c,则a=b=c=(15)若a^2n-1·a^2n 2020-11-27 …
1若x^2=1,则x=1;2若x^2=1,则它的解是x=1;3若x^2=1,则它的解是x=1或x=- 2020-12-13 …