早教吧作业答案频道 -->数学-->
已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.(1)如图①,求∠T和∠CDB的大小;(2)如图②,当BE=BC时,求∠CDO的大小.
题目详情
已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
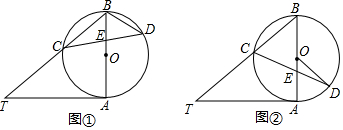
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC时,求∠CDO的大小.
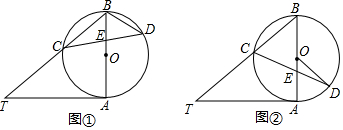
▼优质解答
答案和解析
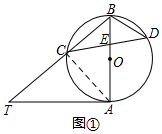 (1)如图①,∵连接AC,
(1)如图①,∵连接AC,
∵AT是⊙O切线,AB是⊙O的直径,
∴AT⊥AB,即∠TAB=90°,
∵∠ABT=50°,
∴∠T=90°-∠ABT=40°,
由AB是⊙O的直径,得∠ACB=90°,
∴∠CAB=90°-∠ABC=40°,
∴∠CDB=∠CAB=40°;
(2)如图②,连接AD,
在△BCE中,BE=BC,∠EBC=50°,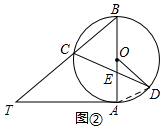
∴∠BCE=∠BEC=65°,
∴∠BAD=∠BCD=65°,
∵OA=OD,
∴∠ODA=∠OAD=65°,
∵∠ADC=∠ABC=50°,
∴∠CDO=∠ODA-∠ADC=65°-50°=15°.
 (1)如图①,∵连接AC,
(1)如图①,∵连接AC,∵AT是⊙O切线,AB是⊙O的直径,
∴AT⊥AB,即∠TAB=90°,
∵∠ABT=50°,
∴∠T=90°-∠ABT=40°,
由AB是⊙O的直径,得∠ACB=90°,
∴∠CAB=90°-∠ABC=40°,
∴∠CDB=∠CAB=40°;
(2)如图②,连接AD,
在△BCE中,BE=BC,∠EBC=50°,

∴∠BCE=∠BEC=65°,
∴∠BAD=∠BCD=65°,
∵OA=OD,
∴∠ODA=∠OAD=65°,
∵∠ADC=∠ABC=50°,
∴∠CDO=∠ODA-∠ADC=65°-50°=15°.
看了 已知AB是⊙O的直径,AT是...的网友还看了以下:
a是b的倍数,c是a的倍数(a、c不相同),下列判断错误的是()A、a与b的和也一定是b的倍数B、a 2020-03-30 …
在长和宽分别是a,b的矩形纸片的四个角都减去一个边长为x的正方形,折起来做成一个没有盖的盒子(1) 2020-05-13 …
如图正方形被一条曲线分成A、B两部分,下面()说法正确.A.如果a>b,那么A周长大于B周长B.如 2020-05-17 …
分解因式(a-b-c)(a+b-c)-(b-c-a)(b+c-a)正确答案是这个:(a+b-c)( 2020-05-17 …
动脑筋答题a的平方+b的平方=c的平方3的平方+4的平方=5的平方5的平方+12的平方=13的平方 2020-05-20 …
行星A和行星B的质量之比MA:MB=2:1,半径之比RA:RB=1:2,两行星各有一颗卫星a和b, 2020-05-21 …
设集合A={x/x-a/<1,x∈R},B={x//x-b/>2,∈R}若A∈B时则a,b必须满足 2020-06-03 …
几道数学题,厉害来!一.代数式3m+2n可以表示什么二.2a-b除以a+b的意义是()A.a与b差 2020-06-03 …
在直角坐标系中,已知线段AB,点A的坐标为(1,-2),点B的坐标为(3,0),如图1所示.(1) 2020-06-14 …
如图,已知一次函数y=kx+b的图像与反比例函数y=8/x的图像交于A,B如图所示,已知一次函数y 2020-06-14 …